Module EA - Examen du 5/1/2004 - Solution
![]()
Transformée de Laplace inverse :
![]() ,
(échelon unité).
,
(échelon unité).
L'intégrale
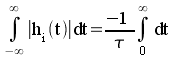 n'est pas bornée : montage instable.
n'est pas bornée : montage instable.
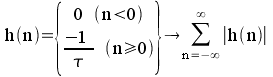 n'est pas bornée : montage instable.
n'est pas bornée : montage instable.
H(n) = 0 pour n<0 : le montage est causal
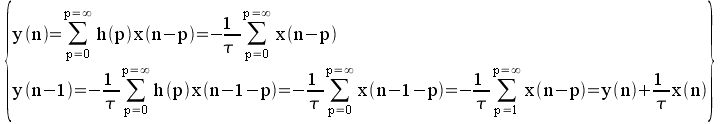
On passe donc de l'échantillon de sortie
numéro n-1 à l'échantillon de sortie numéro
n en ajoutant l'échantillon d'entrée numéro n
(multiplié par
![]() )
: l'équation aux différences est :
)
: l'équation aux différences est :
![]()
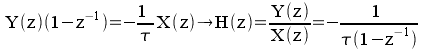
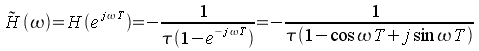
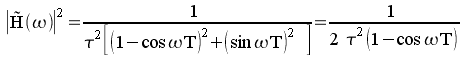
Cette expression tend vers l'infini pour
![]() ,
en particulier pour la fréquence nulle comme pour
l'intégrateur analogique. Elle vaut
,
en particulier pour la fréquence nulle comme pour
l'intégrateur analogique. Elle vaut
![]() pour
pour
![]() ,
en particulier pour
,
en particulier pour
![]()
Réponse impulsionnelle finie, donc stable.
H(n)=0 pour n<0 : système causal.
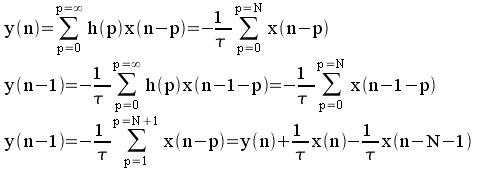
d'où l'équation aux différences :
![]()
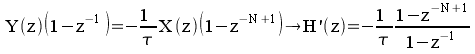
![]()
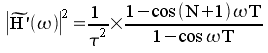
Cette fonction ne tend pas vers l'infini à
la fréquence nulle, mais vaut
![]()
La figure ci-dessous représente les variations du carré du module du gain complexe, normalisé par rapport à 1/t, pour N=5, comparé avec le filtre à RII
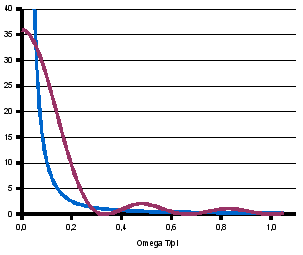

.![]() (voir la figure)
(voir la figure)
![]()
![]()
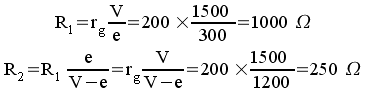
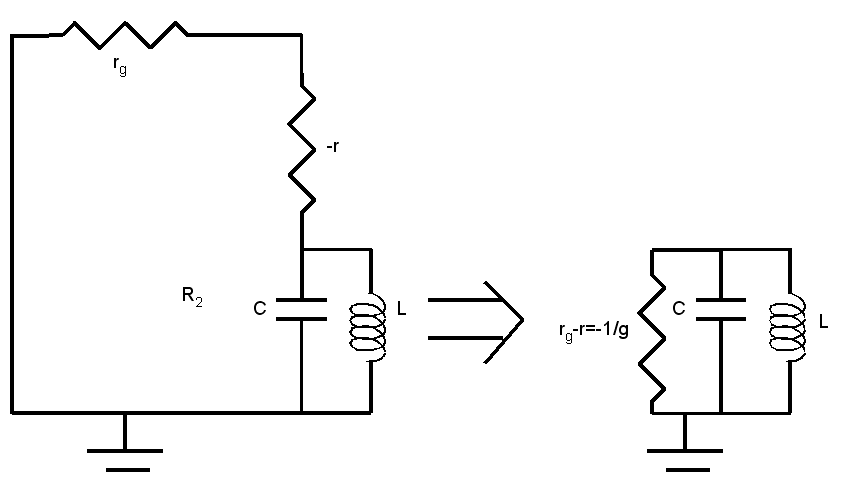
Ce
modèle est imparfait car il ne tient pas compte des pertes (en
particulier dans la bobine puisqu'on a négligé sa
résistance). On peut en tenir compte en introduisant une
résistance R=1/G en parallèle avec cette bobine, donc
avec l'ensemble. On est alors ramené au schéma vu en
cours :
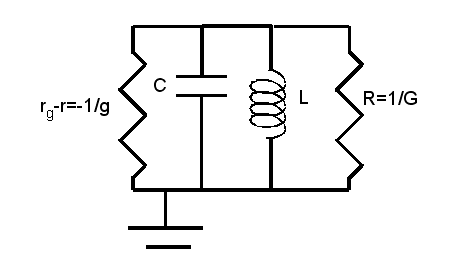
Voir le cours. Impédance Z par exemple (autres approches possibles)
![]() ou bien :
ou bien :
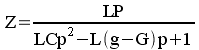 si on tient compte des pertes (ce qui n'était pas demandé)
si on tient compte des pertes (ce qui n'était pas demandé)
Pôles complexes conjugués :
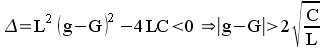 ou
bien
ou
bien
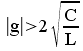
Partie réelle positive :
![]() ou bien
ou bien
![]()
La deuxième condition est satisfaite par construction (avec G = 0). La première impose des limites sur le choix de L et C si r et rg sont imposés
Limite de stabilité : pôles
imaginaires purs de la forme
![]()
Partie réelle du dénominateur nulle
:
![]()
Partie imaginaire du dénominateur nulle :
si G est nulle, il est impossible d'annuler cette partie imaginaire (il faudrait g = 0)
si G n'est pas nulle (on tient compte des
pertes) :
![]()
On fera l'application numérique pour L = 0,2 mH et C = 10 pF
![]()
![]()
V = V0 donne :
![]() r est la valeur calculée ci-dessus.
r est la valeur calculée ci-dessus.
![]()
Le circuit résonant présente une faible impédance pour les harmoniques de rang supérieur à 1
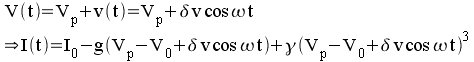
En posant
![]() :
:
![]()
Les harmoniques apparaissent dans les puissances du cosinus :
![]()
![]()
Si on élimine les harmoniques 2 et 3 on a :
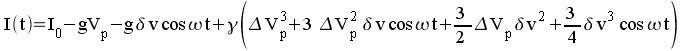
La composante alternative à la fréquence fondamentale est donc :
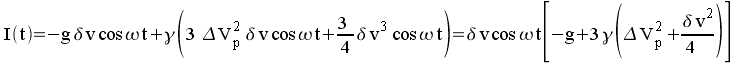
La diode est donc caractérisée par
une admittance
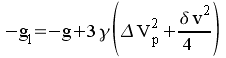
On retrouve la même valeur que pour
l'exemple du cours pour
![]() (polarisation au centre de symétrie de la caractéristique).
(polarisation au centre de symétrie de la caractéristique).
Le système linéaire équivalent
à l'oscillateur en régime établi, dans
l'approximation du premier harmonique, satisfait le critère de
Barkhausen (il est à la limite de l'oscillation). Il faut donc
tenir compte des pertes, matérialisées par R (ou G)
dans les réponses précédentes, sinon on ne peut
être à la limite de stabilité que pour
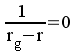 ,
ce qui n'est pas réalisable.
,
ce qui n'est pas réalisable.
La fréquence d'oscillation est donc celle
calculée dans la partie A :
![]()
L'amplitude est donnée par la relation
trouvée dans la partie A :
![]() où r est donné par
où r est donné par
![]()
On peut donc écrire :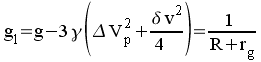 ,
ce qui donne la valeur de l'amplitude de l'oscillation dv
:
,
ce qui donne la valeur de l'amplitude de l'oscillation dv
: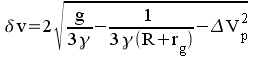
Comme pour la partie A :
![]()
Si on néglige les pertes dans la bobine (R
très grand ) :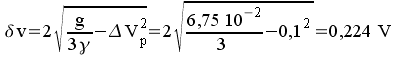
La tension de polarisation permet de contrôler l'amplitude (par l'intermédiaire de Dvp)
Varicap (voir le cours)