Solution

1 Filtre actif

a Filtre passe haut

i Cahier des charges

ii Filtre passe bas prototype

Sur l'axe des pulsations (ou fréquences) réduites : 1, 2 ()

Sur l'axe du carré du module du gain complexe : -20 dB, - 3 dB, 0 dB

iii Fonction d'approximation du passe bas prototype

iii.1 Quelle est la forme générale de la fonction d'approximation d'un filtre de Butterworth ?

Paramètres , n. L'ordre du filtre est donné par n

iii.2 Paramètres de la fonction d'approximation du filtre passe bas prototype

Coupure à 3 dB : (voir le cours)

pour on doit avoir , soit soit

La plus petite valeur de n qui satisfait cette inégalité est 4

L'ordre est égal à n=4

iv Fonctions de transfert du passe bas prototype

Voir le cours pour la justification de la démarche :

pôles solutions de

soit

Il y a donc 4 pôles sur le cercle trigonométrique du plan de la variable complexe s :

On retient les pôles à partie réelle négative

v Fonction de transfert du filtre passe haut

v.1 Fonction de transfert en s

On applique la transposition

v.2 Fonction de transfert de la variable de Laplace p

( défini à la première question)

b Circuit

i Quadripôles Q1 et Q2

i.1 Quadripôle Q1

où v₀ est la tension au point commun des condensateurs :

On a donc :

Le quadripôle est symétrique :

i.2 Quadripôle Q2

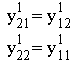
où v₀ est la tension au point commun des résistances :

On a donc :

Le quadripôle est symétrique :

ii Montage

ii.1 Gain en tension en fonction des paramètres y des quadripôles

On remarque que v-=0 (amplificateur parfait) : le courant i₂¹ du quadripôle Q1 est :

et le courant i₁² du quadripôle Q2 est :

On a de plus :

(amplificateur parfait)

On a donc :

ii.2 Gain en tension en fonction des composants

On pose dans les quadripôles :

On a donc :

et

ou bien :

ii.3 Propriétés du montage

Comportement asymptotique aux fréquences basses :

Comportement asymptotique aux hautes fréquences :

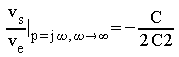
C'est donc un filtre passe haut, d'ordre 2 (pente )

ii.4 Utilisation du montage

1. On peut ajuster les paramètres pour se ramener à chacun des deux facteurs du filtre passe haut de Butterworth ci-dessus (à une constante près).

2. Deux cellules sont nécessaires puisque le filtre à construire est du quatrième ordre.

3. Par identification :
   pour l'une des cellules
   pour l'autre cellule
   ce qui donne les relations :
   pour l'une des cellules
   pour l'autre cellule
   3 relations, 3 paramètres C, C2, R pour chaque cellule. Il faudra éventuellement une cellule inverseuse selon le signe que l'on veut obtenir.

2 Filtres échantillonnés

a Séquences et échantillons

i Définitions

1. Voir le cours

2. Voir le cours

3. Voir le cours

4. Réponse impulsionnelle, voir le cours

ii Séquence retardée.

b Fonction de transfert en z

i Définitions

ii Séquence retardée

iii Exercice 1

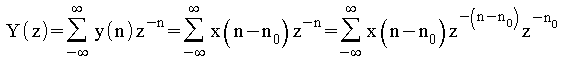
1. Transformée en z de l'équation aux différences :
   
   
   

2. Un seul pôle : stable pour

3. 

4. 
   Pour :Fonction décroissante, valeur 1 à l'origine, 1/25 pour :
   

5. 
   
   Remarquer que la somme des échantillons de h(n) ne converge pas si a > 0

iv Exercice 2

1. Comme ci-dessus :
   
   
   

2. Ce système est-il stable ?
   Pôles racines de , soit :
   
   
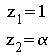
   Un des pôles est toujours de module égal à 1 : instable.