L’une portant sur la réponse impulsionnelle h(t) de ce système.
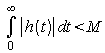où
M est finie
L’autre portant sur la fonction de transfert H(p) de ce système.
Tous ses pôles ont une partie réelle négative
Rappeler les conditions nécessaires et suffisantes pour qu’un système soit stable :
L’une portant sur la réponse impulsionnelle h(t) de ce système.
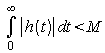où
M est finie
L’autre portant sur la fonction de transfert H(p) de ce système.
Tous ses pôles ont une partie réelle négative
Comment calcule-t-on le gain en boucle ouverte d’un système dont on connaît la fonction de transfert ?
C'est le dénominateur de cette fonction de transfert -1
Expliquer comment le critère de Nyquist permet de connaître le nombre de pôles à partie réelle positive d’une fonction de transfert.
En particulier, détaillez les informations qui doivent compléter celle(s) données par le critère de Nyquist.
Il donne la différence entre le nombre de zéros à partie réelle positive et le nombre de pôles à partie réelle positive du dénominateur de la fonction de transfert.
Pour conclure quant à la stabilité, il faut donc connaître en plus
le nombre de pôles à partie réelle positive de ce dénominateur,
le nombre de pôles à partie réelle positive du numérateur
(on suppose qu'il n'y a ni pôles ni zéros communs au numérateur et au dénominateur)
À quelle condition un système instable montre-t-il un comportement oscillatoire quasi sinusoïdal ?
Il faut qu'il possède au moins une paire de pôles complexes conjugués
Calculer la fonction de transfert du circuit de la figure 1.
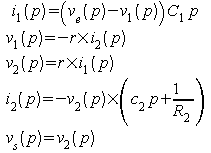
ce qui donne (et c'est facile avec le graphe de fluence !) :
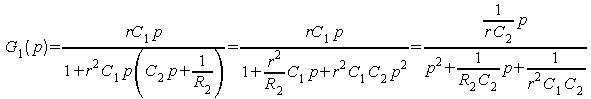
Montrer
que cette fonction de transfert peut s’écrire sous la
forme suivante :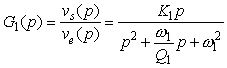
C'est la forme de la deuxième expression trouvée ci-dessus.
Calculer les paramètres K1, w1 et le facteur de qualité Q1 de ce circuit en fonction de r, C1, C2, R2.
Par identification :
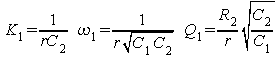
r = 1 kW, R2=10 kW, C1=1 nF, C2=100 nF.
Donner les valeurs numériques de K1, w1 et Q1
Le circuit de la figure 1 est utilisé pour fabriquer un oscillateur selon le montage de la figure 3. Dans ce montage, k est un amplificateur de tension idéal (impédance d’entrée infinie, impédance de sortie nulle, gain indépendant de la fréquence) de gain en tension réel k.
Calculer le gain en boucle ouverte GBO(p) du montage de la figure 3.
Mise en équation :
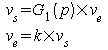
Avec l'aide du graphe de fluence, on verrait immédiatement
que
.
Sans l'aide du graphe de fluence, il faut imaginer une entrée
quelque part dans le circuit, entrée que l'on attaque avec une
tension nulle :
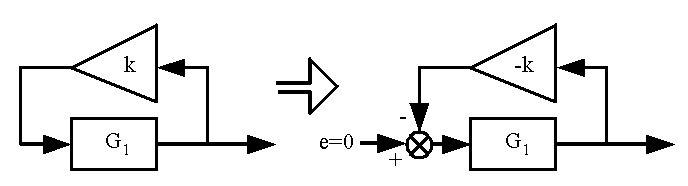
La fonction de transfert est alors
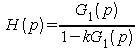et le gain en boucle ouverte s'en déduit.
Le lieu de Nyquist de
est
un cercle centré sur l'axe réel, passant par les points
(pour
)
et
(pour
).
Le lieu du gain en boucle ouverte est donc également un cercle
centré sur l'axe réel, à droite ou à
gauche de l'origine selon le signe de
.
Avec les valeurs numériques, on a
.
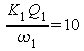Le lieu de Nyquist entoure le point critique si
(
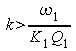pour
les valeurs numériques ci dessus).
Exprimer la condition que doit satisfaire le gain k de l’amplificateur de tension pour qu’une oscillation prenne naissance dans le circuit.
Le lieu de Nyquist entoure le point critique si
(
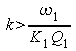pour
les valeurs numériques ci dessus).
Les pôles de la fonction de transfert sont complexes
conjugués (comportement oscillatoire) si
environ (pour les valeurs numériques ci-dessus)
Quelle est la fréquence f0 de cette oscillation lorsque l’on est à la limite du comportement oscillatoire ?
Condition limite pour
,
on a alors les pôles complexes conjugués
.
La fréquence de cette oscillation est donc
Calculer l’amplitude S et la fréquence f de l’oscillation lorsque le régime stabilisé est atteint.
Régime stabilisé : 
ce qui donne 