Examen partiel du 17/11/2000

Corrigé

Première épreuve : électronique analogique

Somme et différence

Tracer le graphe de fluence représentant le fonctionnement du montage.

Figure 1

En déduire l’expression des gains

Donner l’expression limite de ces gains

si , alors

et .

Filtre

Faire le graphe de fluence du montage.

Figure 2

En déduire le gain en boucle ouverte Gbo(p)

Stabilité déduite de Gbo(p)

Figure 3

Le gain en boucle ouverte contient un pôle en p = 0. On contourne ce pôle par un demi-cercle de rayon e aussi petit que nécessaire. La variable complexe p vaut alors , avec .

Alors varie comme , avec variant de p à -p. D’où la courbe :

Figure 4

Elle n’entoure pas le point critique. Pas de pôles à partie réelle positive pour , donc pas de zéros à partie réelle positive pour le dénominateur des fonctions de transfert.

Gains du montage de la figure 2

Stabilité déduite du dénominateur

, étude de D(p) = 0. La somme des racines est négative dans tous les cas, leur produit est positif dans tous les cas : pôles réels négatifs ou complexes conjugués à partie réelle négative : stable.

Oscillateur

Gain en boucle ouverte T(p)

Graphe de fluence presque identique, à un signe près :

Figure 5

Gain en boucle ouverte presque identique, à un signe près (mais qui change tout) :

Stabilité

Rien de changé autour du pôle à l’origine. Au contraire, la phase de la courbe de Bode est modifiée à cause du signe.

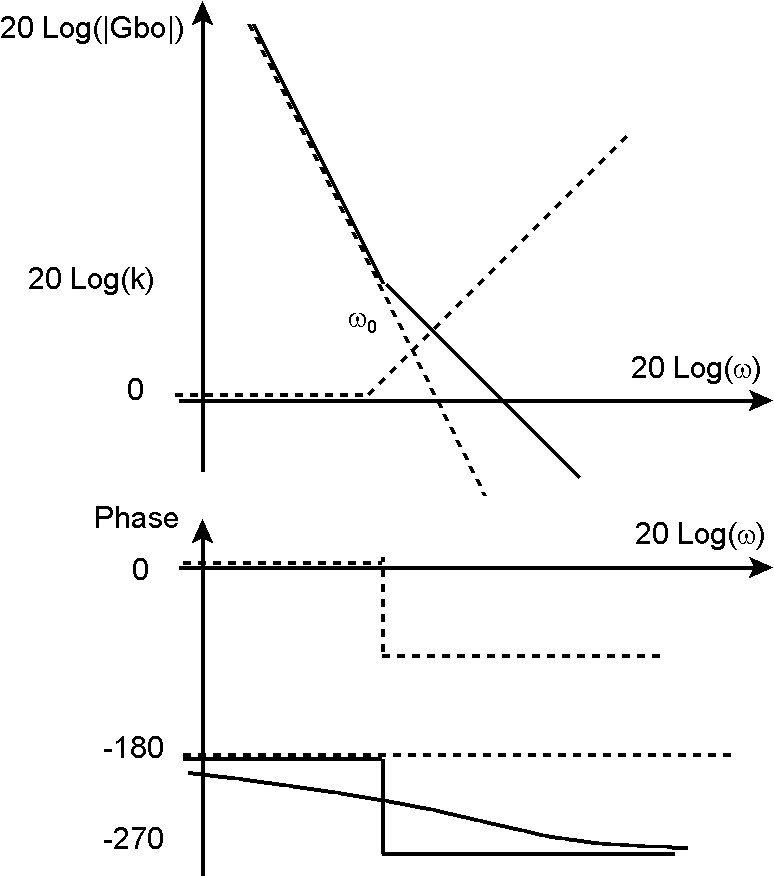
Figure 6

Figure 7

Cette fois-ci, la courbe entoure 2 fois le point critique : les fonctions de transfert ont deux pôles à partie réelle positve.

Gains du montage de la figure 3

Oscillateur

La somme des racines de l’équation qui annule le dénominateur est positive. Le produit des racines est aussi positif : les racines sont soit réelles positives, soit complexes conjuguées à partie réelle positive. Pour un comportement oscillatoire, il faut des racines complexes conjuguées, donc un déterminant négatif :

sera négatif si .

Remarquer que la partie réelle des pôles ne peut s’annuler (sauf pour ou qui ne sont pas des conditions acceptables) : on ne peut pas atteindre un régime stabilisé . Il ne s’agit pas d’un bon oscillateur.