Commentaires

Gain en boucle ouverte

Pour ce qui nous concerne, c'est-à-dire l'étude de la stabilité, la notion de gain en boucle ouverte est venue lorsque l'on a cherché à étudier le dénominateur des fonctions de transfert ou immittance.
Souvenez-vous de la démarche : trouver si les valeurs de la variable complexe p qui annulent le dénominateur de ces fonctions de transfert ou immittance ont leur partie réelle positive ou non. Pour cela :

On applique le théorème de Cauchy à ce dénominateur, en faisant suive au point représentatif de p le contour de Bromwich (qui entour toute la région du plan p où la partie réelle est positve). On étudie alors le lieu du point représentatif de la fonction de transfert ou immittance par rapport à l'origine.
Par référence aux systèmes bouclés les plus simples, où l'on peut facilement identifier la chaîne d'action (fonction de transfert A(p)) et la chaîne de réaction (fonction de transfert B(p)), donc la boucle et le gain en boucle ouverte T(p)=A(p).B(p), on enlève à ce dénominateur, ce qui donne T(p) et on étudie T(p) par rapport au nouveau point critique [-,0].

Il existe bien sûr des cas moins simples, et le sujet du partiel en est un, où il est un peu plus difficile d'identifier le gain en boucle ouverte, au sens géométrique (où est la boucle sur le schéma ?) du terme.
Néanmoins, la démarche mathématique reste la même : il faut étudier la courbe représentative du dénominateur -1 par rapport au point critique, et on continue à appeler ce dénominateur -1 "gain en boucle ouverte.
Pour vous rassurer, vous pouvez transformer le schéma bloc du montage pour lui donner la forme d'une boucle simple {A,B}, sachant que ce travail est fastidieux et inutile pour ce qui concerne le problème.
Voici un exemple des étapes de cette transformation. "Int" représente l'intégrateur.
Schéma initial :

On rentre le facteur k dans la boucle :

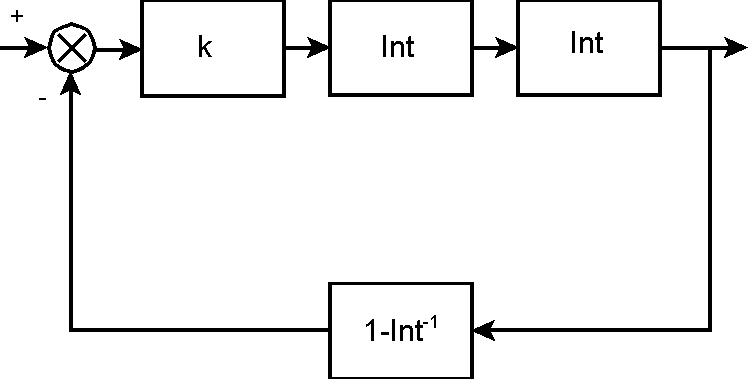
On déplace une boucle ce qui fait apparaître la fonction inverse de l'intégrateur Int^-1 :

On somme les deux branches parallèles :

Ontransforme le sommateur en comparateur :

On trouve ainsi le schéma simple avec
A=k.Int.Int, B=1-Int^-1 et
T=AB=k.Int.Int-k.Int
Int, le gain des intégrateurs, est

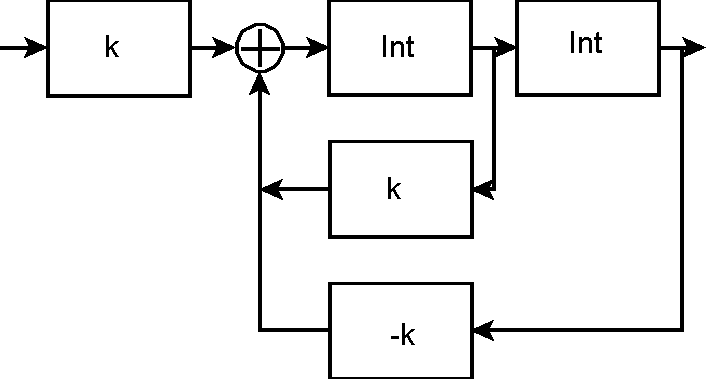
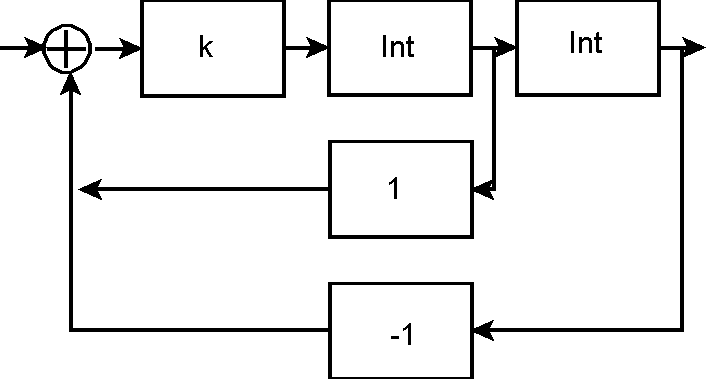
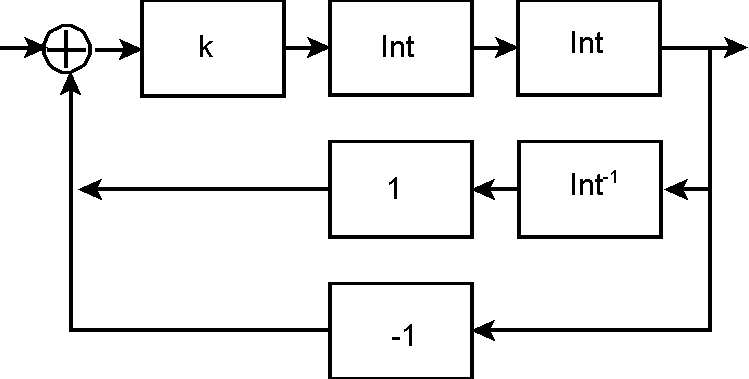
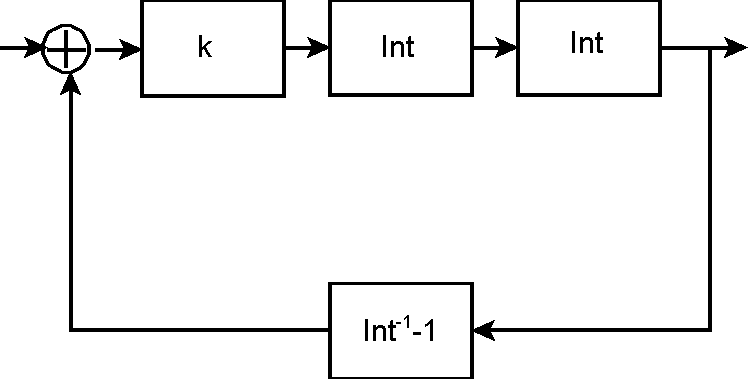
, ce qui donne bien le résultat obtenu directement