Filtres échantillonnés

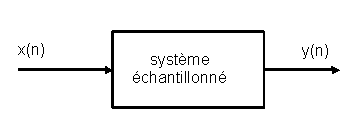
Il s'agit de dispositifs linéaires destinés à traiter des signaux dont la valeur n'est connue qu'à des instants discrets. Ils seront représentés par une séquence de nombres, plutôt que par une fonction du temps comme dans le cas des dispositifs à temps continu. Ces séquences résultent souvent de la prise d'échantillons à des instants réguliers d'un signal continu. L'entrée des systèmes échantillonnés est attaquée par une séquence, ils délivrent ne séquence à la sortie :

I Introduction

L'intervalle de temps entre deux prises d'échantillons est la période d'échantillonnage (notée T dans ce texte), inverse de la fréquence d'échantillonnage.

Les échantillons sont numérotés à partir d'une origine arbitraire et seront notés x(n) où n est le numéro de l'échantillons.

Une séquence d'échantillons x(n) sera notée : {x(n)} ou plus simplement, lorsqu'aucune confusion n'est possible entre un échantillon et la séquence complète : x(n)

Les dispositifs étudiés reçoivent en entrée une séquence {x(n)} et délivrent en sortie une séquence {y(n)}

I.1 Linéarité et invariance

Les systèmes que nous étudierons possèdent les deux propriétés suivantes :

• ils sont linéaires : si {y1(n)} est la séquence délivrée en sortie en réponse à la séquence d'entrée {x1(n)} et {y2(n)} la séquence délivrée en sortie en réponse à la séquence d'entrée {x2(n)}, alors la séquence délivrée en sortie en réponse à toute combinaison linéaire d'entrée :
  {a x1(n)+b x2(n)}=a {x1(n)}+b {x2(n)}
  est la combinaison linéaire
  {a y1(n)+b y2(n)}=a {y1(n)}+b {y2(n)}
  (on a défini au passage ce qu'est une combinaison linéaire de deux séquences : c'est la séquence dont chaque échantillon est combinaison linéaire des deux échantillons correspondant - même numéro - des deux séquences)

• ils sont invariants dans le temps, c'est à dire que leurs propriétés restent identiques au cours du temps.
  Cela se traduit de la façon suivante :
  si {y(n)} est la réponse à {x(n)}, alors la réponse à {x1(n)}={x(n-n0)}, séquence déduite de la précédente par une translation temporelle de n0 échantillons, est {y1(n)}={y(n-n0)}, c'est à dire la réponse à la première séquence, décalée du même nombre d'échantillons

I.2 Les séquences existent-elles ?

a Techniques numériques

Si des techniques numériques sont utilisées, elles traitent en effet des séquences de nombres :

• soit issus en temps réel d'un processus réel, lui-même numérique ou analogique. Dans ce dernier cas, il aura fallu convertir au préalable le signal analogique en nombre. Cette conversion se fait à des instant discrets,

• soit issu d'un enregistrement préalable de valeurs (temps différé) obtenues également à des instants discrets

II Caractérisation des systèmes échantillonnés linéaires et invariants dans le temps.

Comme les systèmes à temps continus, ils peuvent être caractérisés de plusieurs façons.

a Définition

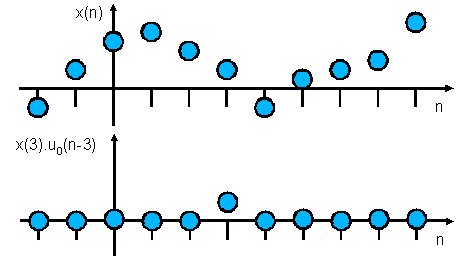
C'est la réponse à une séquence particulière appliquée en entrée, la séquence "impulsion unité".

i Séquence impulsion unité

Tous les échantillons de cette séquence sont nuls, sauf l'échantillon numéro 0 qui vaut 1 :

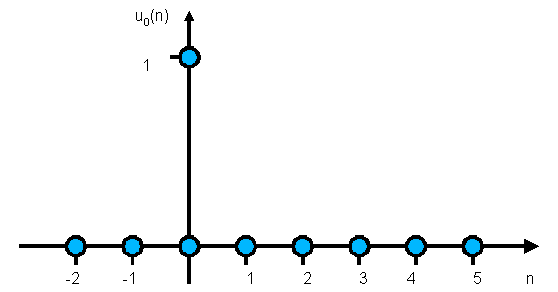
La séquence

ii Réponse impulsionnelle d'un système

c'est la séquence délivrée par le système en réponse à la séquence impulsion unité appliquée en entrée.

Exemple d'une réponse impulsionnelle :

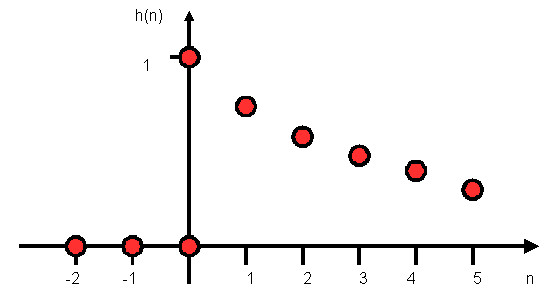
La réponse à cette séquence

b Propriétés

L'intérêt de la réponse impulsionnelle est qu'elle permet de prévoir la réponse du système à n'importe quelle séquence d'entrée.

i Réponse à une séquence quelconque {x(n)}

Elle s'exprime par une relation simple entre les échantillons de cette séquence d'entrée et ceux de la réponse impulsionnelle (relation de convolution discrète) :

Dans ces relations, h(k) est la réponse impulsionnelle.

La démonstration de cette relation repose sur la linéarité et l'indépendance temporelle :

i.1 La séquence d'entrée est une combinaison linéaire de séquence impulsion unité.

Chacune de ces séquences est décalée et multipliée par une constante :

Dans cette expression, est la séquence impulsion unité décalée de p échantillons.

puisque le système est invariant dans le temps, sa réponse à l'impulsion unité décalée est la réponse impulsionnelle décalée de la même quantité, et puisqu'il est linéaire, la réponse à une combinaison linéaire de séquences d'entrée est la même combinaison linéaire des séquences de sortie.

On a donc les correspondances suivantes entre entrée et sortie :

et chaque échantillon de la séquence de sortie est par conséquent égal à :

Cette relation peut s'écrire sous sa forme symétrique en posant :

ii Causalité

ii.1 Définition

Un système est causal si dans la description de son fonctionnement aucune cause ne précède ses effets. Le monde réel est causal mais on peut envisager des systèmes échantillonnés non causaux dans la mesure ou le rang des échantillons dans une séquence n'est pas obligatoirement lié à l'écoulement du temps réel. C'est le cas par exemple si le système ne travaille pas en temps réel mais travaille sur des données acquises au préalable (fichier de données).

ii.2 Expression

Le caractère causal ou non causal d'un système se déduit simplement de sa réponse impulsionnelle :

• sialors le système est causal puisque le calcul d'un échantillon de rang donné n de la sortie (l'effet) ne fait intervenir que des échantillons de l'entrée (la cause) de rang avec , donc antérieurs.

• dans le cas contraire, le calcul d'un échantillon de rang donné de la sortie fait intervenir au moins un échantillon "futur" de l'entrée, et le système n'est pas causal.

iii stabilité

iii.1 Définition

Un système est stable si la grandeur de sortie reste finie en valeur absolue quelle que soit la grandeur finie en valeur absolue appliquée en entrée :

tel que si alors

iii.2 Expression

Une condition nécessaire et suffisante pour qu'un système soit stable est donnée par sa réponse impulsionnelle :

La condition est nécessaire :

Soit la séquence d'entrée définie pour toute valeur du rang n par . On a alors, si :

Cette quantité doit être finie, donc la condition ci-dessus est nécessaire.

La condition est suffisante :

Quelle que soit la séquence d'entrée bornée en valeur absolue par le réel M, on peut écrire successivement:

et la condition est bien suffisante

iv Les deux familles de filtres échantillonnés

On distingue deux groupes de filtres échantillonnés, selon que la réponse impulsionnelle contient ou non un nombre fini d'échantillons non nuls.

iv.1 Filtres à réponse impulsionnelle finie (RIF, filtres non récursifs)

Par définition, la réponse impulsionnelle de ces filtres contient un nombre fini d'échantillons non nuls. Ces filtres possèdent par conséquent certaines propriétés :

• Ils peuvent être matérialisés, qu'ils soient causaux ou non, par un nombre fini d'opérations arithmétiques (additions et multiplication) et de retard (mémorisation). Ils sont donc toujours réalisables (en temps différé seulement s'ils ne sont pas causaux)

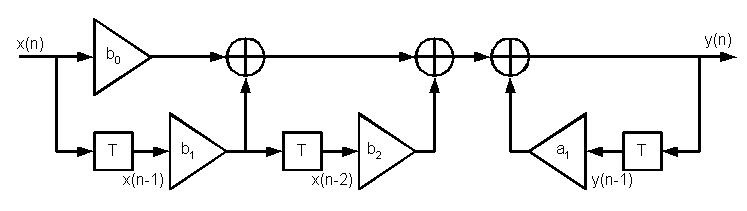
L'exemple ci dessus décrit le filtre dont la réponse impulsionnelle ne contient que les échantillons non nuls h(0), h(1), h(2). Le bloc T représente un retard d'une période d'échantillonnage, les triangles représentent des multiplications par la quantité indiquée.

• Ils sont toujours stables, puisque la somme finie des échantillons de leur réponse impulsionnelle est finie.

• Ils sont causaux ou non causaux, selon qu'il existe ou non des échantillons de rang négatif dans la réponse impulsionnelle.

c Exemple : moyenne sur 5 échantillons

Soit le filtre défini par l'opération suivante, qui réalise la moyenne de 5 échantillons d'entrée pour calculer la sortie :

Cette expression est l'expression de la sortie par une convolution discrète faisant intervenir la réponse impulsionnelle, avec

Il s'agit donc d'un filtre à réponse impulsionnelle finie (5 échantillons non nuls dans la réponse impulsionnelle), donc stable et réalisable , non causal (des échantillons de rang négatif dans la répons impulsionnelle : le filtre n'est pas réalisable en temps réel, il faudrait connaître deux échantillons futurs de l'entrée).

II.2 Équation aux différences

a définition

Le système est caractérisé par une équation qui donne chaque échantillon de rang n de la sortie en fonction

• d'un nombre fini d'échantillons d'entrée et

• d'un nombre fini d'échantillons de sortie de rang différent de n

Les deux sommes sont finies, ce qui garantit que le système est réalisable avec un nombre fini d'opérations arithmétiques et de retards.

Les différences entre les échantillons de sortie à des instants différents interviennent dans cette équation, d'où son nom.

b Commentaires

i Conditions initiales

L'équation à elle seule ne suffit pas à calculer pour toute valeur de n. Il faut en effet pour démarrer le calcul (par exemple calculer ) connaître les valeurs des échantillons de sortie à droite du signe =. Ce sont les conditions initiales qui doivent donc être en nombre égal au nombre d'échantillons de sortie qui figurent dans le membre de droite ordre de l'équation).

ii Cas particulier : la sortie n'intervient pas dans le membre de droite

Dans ce cas, l'équation se réduit à une convolution discrète entre l'entrée et la séquence bi Cette séquence représente donc la réponse impulsionnelle du système, qui est donc finie par construction. Inversement, si le système est à réponse impulsionnelle finie, les échantillons de sortie s'expriment par cette convolution et tous les coefficients sont nuls : une équation aux différences complète (échantillons de sortie dans le membre de droite) représente donc nécessairement un filtre à réponse impulsionnelle infinie (ou récursif : l'équation aux différences est une équation récursive si les échantillons de sortie sont présents dans le membre de droite).

iii Matérialisation

Tout filtre défini par une équation aux différences peut être matérialisé avec un nombre fini d'opérations arithmétiques et de retards. La figure montre le cas où il y a deux valeurs non nulles pour lescoefficients et une valeur non nulle pour les coefficients

iv Trouver la réponse impulsionnelle à partir de l'équation aux différences

iv.1 Principe

Si l'équation aux différences n'est pas une vraie équation récursive, on a vu qu'elle donne directement les valeurs des échantillons de la réponse impulsionnelle (finie). Si c'est une vraie équation récursive, on peut reconstituer la réponse impulsionnelle échantillon par échantillon en imaginant que la séquence d'entrée est la séquence qui vaut zéro pour toutes les valeurs de n sauf pour n = 0.

iv.2 Exemple

On prend l'équation correspondant à la figure ci-dessus :

Il faut une condition initiale, puisqu'un échantillon de sortie figure à droite. On prend .

La séquence d'entrée est l'impulsion unité.

On peut alors calculer :

c exemple : intégration par la méthode des trapèzes

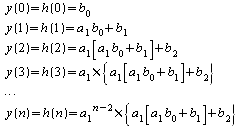
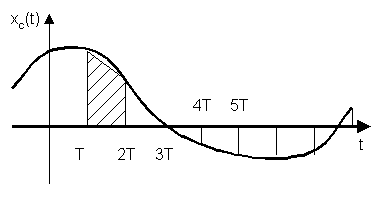
Soit le filtre défini par l'opération suivante, qui réalise l'approximation du calcul de l'aire sous une courbe continue par la méthode des trapèzes. On ne connaît que les échantillons de cette fonction et l'aire sous sa courbe entre deux instants d'échantillonnage et est approchée par l'aire du trapèze (voir la figure). L'aire totale entre l'instant origine (c'est la condition initiale) et l'instant peut donc s'exprimer par la forme récursive :

qui exprime qu'on a ajouté à l'aire précédente la valeur de l'aire du trapèze entre et . C'est donc bien une équation aux différences et un filtre récursif (RII)

On peut, comme montré ci dessus, retrouver la réponse impulsionnelle de ce filtre, en l'attaquant par la séquence , avec la condition initiale

On constate que ce filtre n'est pas stable.

II.3 Fonction de transfert en z

a transformée en z

i définition

La transformée en z d'une séquence est donnée par :

c'est une fonction de la variable complexe z.

ii propriétés

ii.1 Cette transformation est linéaire

On vérifie facilement que si l'on a

alors

ii.2 Transformée d'une séquence retardée de n₀ échantillons

Si est la séquence déduite de la séquence par décalage de échantillons, on a

En effet, ce qui peut s'écrire, avec le changement de variable :

ii.3 Produit de convolution produit simple

Si une séquence est la convolution discrète de deux autres séquences, sa transformée en z est le produit simple des transformées en z de ces séquences :

b Fonction de transfert en z

i Définition

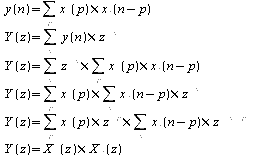
La fonction de transfert en z d'un filtre échantillonné est la transformée en z de sa réponse impulsionnelle.

Elle peut donc s'écrire :

ii propriétés

ii.1 Linéarité

On vérifie facilement que cette transformation est linéaire

ii.2 Expression de la transformée en z de la sortie

Puisque la séquence de sortie est la convolution discrète de la séquence d'entrée et de la réponse impulsionnelle, la transformée en z de la sortie est le produit simple de la transformée en z de la séquence d'entrée et de la fonction de transfert en z.

ii.3 Cas particulier : z=e^pT

où p est une variable complexe. On trouve dans ce cas où l'on reconnaît la transformée de Laplace de la distibution qui représente souvent un signal échantillonné.

iii Calcul de la fonction de transfert en z

Il peut se faire à partir de l'équation aux différences ou de la réponse impulsionnelle. Dans les deux cas on utilise la linéarité et la propriété de retard.

iii.1 À partir de l'équation aux différences

Exemple (intégration) :

On prend la transformée en z de chaque terme et on obtient :

ce qui s'écrit :

ce qui donne :

iii.2 À partir de la réponse impulsionnelle

On calcule directement la transformée en z de cette réponse impulsionnelle, ce qui conduit facilement à un résultat si cette réponse est finie.

Exemple (moyenne sur 5 échantillons) :

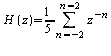ce qui peut s'écrire en posant :

où l'on reconnaît la somme d'une progression géométrique :

On a donc ici (avec et ) :

II.4 gain complexe

Comme pour les circuits à temps continu, le gain complexe indique comment sont transformées les composantes spectrales du signal par le filtre, et est un cas particulier de la fonction de transfert en z.

a Transformée de Fourier discrète

i définition

La transformée de Fourier d'une séquence est donnée par :

C'est une fonction de la variable réelle

ii propriétés

ii.1 Cas particulier de la transformée en z

Soient et la transformée en z et la transformée de Fourier de la séquence

. On a :

La transformée de Fourier est donc la transformée en z pour z placé sur le cercle de rayon unité du plan complexe et on peut écrire

ii.2 périodicité

La fonction est périodique en , de période . En effet, l'exponentielle complexe reprend la même valeur si est incrémenté d'un multiple entier de

ii.3 symétries

On peut écrire

Si la séquence x(n) est réelle, on voit sur cette expression que la partie réelle de la transformée de Fourier est :

et est paire en , de la même façon sa partie imaginaire est

et est impaire en

ii.4 Conclusion

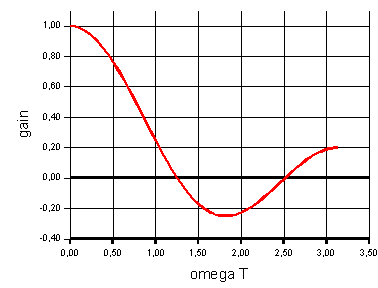
Cette fonction continue est entièrement connue si on la connaît sur une demi-période, par exemple entre 0 et . L'autre demi-période est déduite par symétrie, et les autres périodes sont identiques à cette première période. Le dessin représente la partie réelle (rouge) et la partie imaginaire (bleue) d'une telle fonction.

ii.5 transformée inverse

On reconnaît dans la définiton de la transformée de Fourier le développelent en série de Fourier de la fonction périodique dont les coefficients sont les échantillons . On peut donc écrire chacun de ces coefficients comme une composante de Fourier de :

ii.6 échantillonnage d'un signal continu (Shannon)

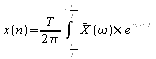
Une situation fréquente est celle où la séquence est déduite d'une fonction à temps continu par échantillonnage aux instants . Il est alors important de connaître la correspondance qui existe entre la transformée de Fourier du signa continu et celle de la séquence.

On part des définitions suivantes pour la signal continu :

• la fonction continue du temps :

• chaque échantillon : : c'st la valeur du signal continu à l'instant

• les relations de transformation de Fourier dans le domaine du temps continu ( est la transformée de Fourier du signal continu) :
  

en écrivant que l'échantillon est la valeur de la fonction continue pour on a :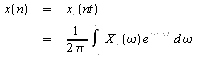

On découpe alors l'axe des pulsations en segments de longueur et l'intégrale sur la pulsation en une somme (infinie) d'intégrales sur des domaines centrés sur et de longueur :

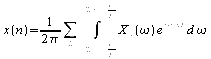
On fait le changement de variable

ce qui donne

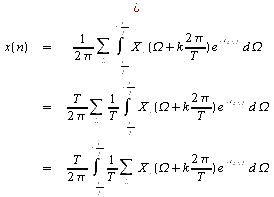
Mais par définition :

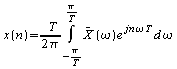
On a donc par identification :

ii.7 Convolution et produit simple

Puisque la transformée de Fourier est un cas particulier de la transformée en z, elle transforme également la convolution de deux séquences en produit de leurs transformées de Fourier.

b Gain complexe

i définition

C'est la transformée de Fourier de la réponse impulsionnelle :

Réciproquement, la réponse impulsionnelle s'exprime à partir du gain complexe :

ii propriétés

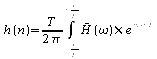
Ce sont celles de la transformée de Fourier d'une séquence :

ii.1 Relation entrée sortie

La convolution : séquence d'entrée – réponse impulsionnelle devient un produit simple :

, ce qui s'écrit

ii.2 Relation avec la fonction de transfert en z

Le gain complexe est un cas particulier de la fonction de transfert en z pour : le point représentatif de z se trouve sur le cercle de rayon unité du plan complexe z (dans le cas du temps continu, le gain complexe est un cas particulier de la fonction de transfert (en p) lorsque le point représentatif de p se trouve sur l'axe imaginaire du plan complexe p).

Il est donc facile d'écrire ule gain complexe si on connaît la fonction de transfert en z.

ii.3 Réponse à une séquence d'entrée harmonique

si la séquence d'entrée est (échantillonnage d'une fonction harmonique de pulsation : ) on a :

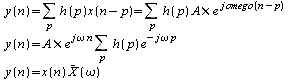
La sortie est également une séquence de même pulsation et la valeur du gain complexe pour la pulsation donne l'amplitude et la phase de la sortie par rapport à celles de l'entrée (d'où le nom de gain complexe).

ii.4 périodicité et symétries

Puisque c'est une transformée de Fourier, le gain complexe présente les propriétés de périodicité (période ) et de symétrie (partie réelle paire, partie imaginaire impaire) rencontrées plus haut. Il est en particulier déterminé sur tout l'axe des pulsations si on le connaît dans l'intervalle .

iii exemples

iii.1 Intégration par la méthode des trapèzes

On connaît la fonction de transfert en z, elle-même déduite facilement de l'équation aux différences : . En faisant le changement de variable on obtient alors :

Il est commode de poser , ce qui permet d'écrire ce résultat sous la forme :

La phase de ce gain est constante et égale à et son module tend vers l'infini à la fréquence nulle.

iii.2 Moyenne sur 5 échantillons

On a également déterminé la fonction de transfert, à partir de la réponse impulsionnelle :

; On peut donc écrire :

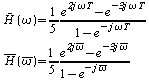en posant comme ci-dessus . On a alors :

, soit :

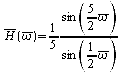ou bien :

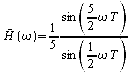
Ce gain est réel, ses variations entre 0 et sont représentées ci dessous : il s'agit d'un filtre passe-bas.