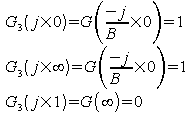| Cahier des charges |
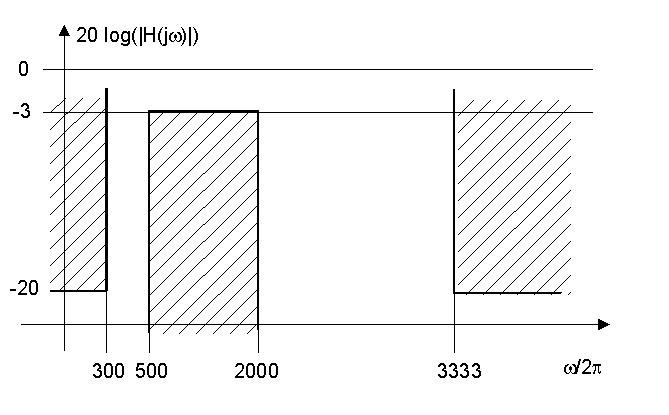
Filtre passe bande, atténuation inférieure
ou égale à 3 dB dans la bande transmise, limitée par
les fréquences 500 Hz et 2 000 Hz, atténuation supérieure
à 20 dB en dessous de 300 Hz et au dessus de 3 333 Hz |
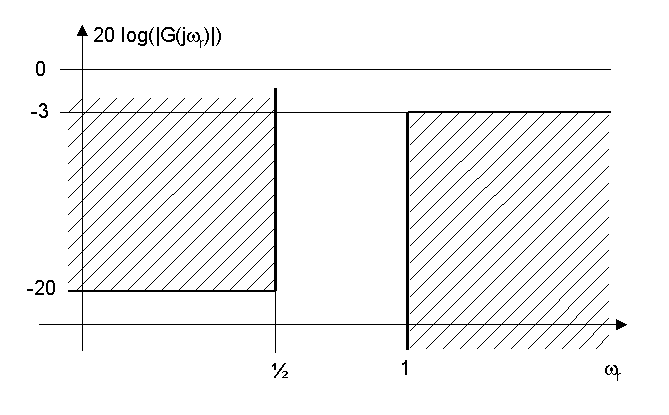
| Gabarit correspondant. Le filtre est bien symétrique.
La fréquence de coupure du passe bas est égale à 1000
Hz, B vaut 1,5 et le facteur k est égal à 2.022 |
 |
| Gabarit en fréquences réduites. On a divisé
les fréquences par 1000 Hz. Ce tracé n'est pas obligatoire
: on possède déjà les valeurs de tous les paramètres
du gabarit du filtre passe bas prototype. |
 |
| Transposition : gabarit du filtre passe bas prototype.
On connait tous les paramètres : a, b, k. On constate qu'on obtient
pratiquement le même prototype que dans l'exemple précédent. |
 |
 fréquence
réduite :
fréquence
réduite :

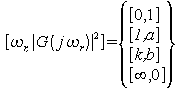
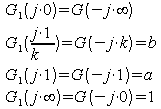 (pourquoi le signe "-" ?)
(pourquoi le signe "-" ?)
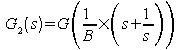
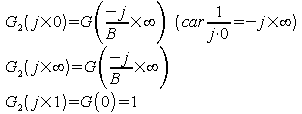
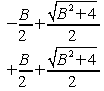 .
Leur différence est donc B, qui est bien la largeur réduite
de bande du filtre passe bande
.
Leur différence est donc B, qui est bien la largeur réduite
de bande du filtre passe bande
 est
un filtre coupe bande dont la largeur de la bande coupée est B
(en pulsation ou fréquence réduite) et dont les paramètres
du gabarit se déduisent simplement de ceux du filtre passe bas par
une démarche identique à celle vue pour le filtre passe bande.
est
un filtre coupe bande dont la largeur de la bande coupée est B
(en pulsation ou fréquence réduite) et dont les paramètres
du gabarit se déduisent simplement de ceux du filtre passe bas par
une démarche identique à celle vue pour le filtre passe bande.