Il est possible de modifier la fréquence d'oscillation (et le spectre de cette oscillation) d'un oscillateur sans agir sur ses composants mais en le synchronisant sur un autre oscillateur. Si la synchronisation se produit, sa fréquence et les propriétés de cette fréquence seront imposées par l'oscillateur synchronisant.
Le signal délivré par l'oscillateur synchronisant est appliqué sur une entrée de l'oscillateur à synchroniser.
On peut représenter le montage par le même schéma que celui qui a été utilisé pour étudier l'effet d'une source de bruit. La source de bruit est remplacée par le signal de synchronisation e(t).
La mise en équation reprend les mêmes étapes :
Nous prenons comme état de référence pour l'oscillateur (indice 0) son état lorsque le signal de synchronisation n'existe pas (e(t)=0).
Le point représentatif de cet état est donné par l'intersection
des deux lieux 
et 
:
La pulsation est 
,
l'amplitude 
et le signal de sortie est, dans le domaine temporel :
Le signal de synchronisation est de la forme 
.
Nous nous plaçons dans le domaine temporel et supposons que la pulsation
du
signal de synchronisation est proche de la pulsation de référence
et
que l'amplitude instantanée de 'oscillation est proche de l'amplitude
de référence 
(le signal de synchronisation n'apporte qu'une faible perturbation)
En présence du signal de synchronisation, le signal de sortie voit son
amplitude et sa fréquence légèrement modifiées par
rapport aux valeurs de référence, et on cherche s'il est possible
que cette fréquence soit égale à 
.
,
où
est
le déphasage entre le signal synchronisé et le signal de synchronisation.
Le circuit peut être décrit par l'équation :
soit
:
ou
:
Dans cette dernière relation, nous faisons l'approximation de remplacer A(V) par A(V0) et l'amplitude de s(t) par son expression de référence V0 à droite du signe égal :
Dans le plan de Nyquist, le membre de gauche de cette relation
désigne un vecteur 
qui
a son origine sur la courbe 
pour 
(c'est notre hypothèse) et son extrémité sur la courbe
.
L'état instantané du système est donc décrit
dans le plan de Nyquist par un vecteur issu du point 
et arrivant sur un point de la courbe 
et tel que la relation ci-dessus soit satisfaite. En particulier la longueur
de ce vecteur est imposée : 
La phase du vecteur se déduit du point imposé (sur la courbe B) et de la longueur imposé.
Il n'y aura de solution que si l'origine du vecteur peut être
placée sur la courbe 
: dans l'exemple ci-dessous, il n'y a pas de solution : l'oscillateur ne peut
être synchroniser. Il faudrait diminuer l'écart entre la fréquence
de synchronisation et la fréquence de l'oscillateur livre, ou augmenter
la longueur du vecteur en augmentant l'amplitude du signa de synchronisation.
En assimilant la courbe B à la perpendiculaire à l'axe réel, on peut écrire la condition de synchronisation
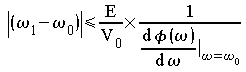
Cette relation donne la condition à satisfaire pour que
la synchronisation puisse avoir lieu, qui fait intervenir la différence
de fréquence et l'amplitude du signal de synchronisation comparée
à l'amplitude de l'oscillateur libre. On constate que la synchronisation
est plus difficile si le circuit sélectif possède un facteur de
qualité élevé (
élevé).
Ce modèle simplifié ne prend pas en compte les effets transitoires. Il permet cependant de prévoir le comportement de l'oscillateur synchronisé : ses écarts (fluctuations) de fréquence contenues dans la plage de synchronisation seront supprimées par la synchronisation si le signal de synchronisation est parfaitement stable. On peut donc s'attendre dans ce cas à un important affinement spectral.
Cette technique est en particulier largement appliquée pour améliorer les propriétés spectrales des lasers de puissance par synchronisation sur un laser de référence.