Il est souvent possible de modifier et de contrôler la fréquence des oscillateurs, soit pour obtenir une accordabilité, soit pour modifier les propriétés d'exactitude, de reproductibilité et de stabilité, soit pour obtenir avec une grande précision une fréquence imposée.
Le principe est simple : agir, par l'intermédiaire d'une grandeur électrique (tension) sur la valeur de certains composants intervenant dans la fréquence de l'oscillation.
On peut rechercher une très grande accordabilité, ou au contraire une accordabilité très limitée destinée seulement à réaliser un réglage fin de la fréquence.
Une très grande accordabilité est facile à atteindre sur un montage multivibrateur (non quasi-sinusoïdal)
Le montage ci-dessous utilise un intégrateur (autour de l'ampli A1) et un trigger de Schmitt (autour de A2). Les deux amplificateurs opérationnels sont alimentés entre 0 et V0. Leurs tensions de saturation en sortie sont 0 et V0.
La rétroaction résistive sur l'entrée + impose un comportement instable : la sortie S ne peut être qu'en saturation (0 ou V0).
Alors l'entrée + est à 2V0/3 et A2 reste dans cet état tant que l'entrée - est à une tension inférieure à cette valeur.
Alors l'entrée + est à V0/3 et A2 reste dans cet état tant que l'entrée - est à une tension supérieure à cette valeur.
Il existe donc pour l'entrée - une plage de fréquences (de V0/3 à 2V0/3) pour laquelle la sortie peut être dans un des deux états stables. La transition d'un état à l'autre se fait pour l'une des deux bornes de ce domaine selon le sens de variation de V-
Sur la figure de gauche, V- part de 0 et croît, sur la figure de droite, V- part de V0 et décroît.
Dans le montage, l'entrée V- de A2 est attaquée par la sortie de A1
Q est un transistor MOSFET à canal n. Il se comporte comme un court-circuit lorsque S = V0 et comme un circuit ouvert lorsque S = 0. L'intégrateur possède donc deux entrées qui sont additionnées avant d'être intégrées, l'une des deux entrées est attaquée par la tension Vc, l'autre est soit à la masse interrupteur fermé, soit en circuit ouvert (interrupteur ouvert).
Lorsque l'interrupteur est ouvert, le gain complexe aux basses fréquences (entre la sortie du montage intégrateur et son entrée Vc) est de la forme (faites le calcul) :
Lorsque l'interrupteur est fermé, ce gain complexe est au contraire :
La tension constante Vc, est donc intégrée dans les deux cas avec la même constante de temps, mais avec un signe différent. La sortie de A1 est donc une tension variant linéairement, avec une pente positive ou négative selon que Q est fermé ou ouvert.
On peut également étudier ce montage en statique ( Vc est constant) :
Si Q est ouvert, alors le courant traversant la résistance R et chargeant le condensateur C est
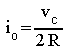et
la sortie de A1 décroît linéairement dans le temps avec
la pente
Si Q est fermé, le courant de charge est la somme des courants traversant les deux résistances R et R/2 :
La tension de sortie de A1 croit donc linéairement avec la pente :
Imaginons l'état initial suivant : la sortie de A1 vaut 0, la sortie de A2 se sature donc à V0 et l'interrupteur est donc fermé. La tension de sortie de A1 croit donc linéairement. Lorsqu'elle atteint la valeur 2V0/3, la sortie de A2 bascule à 0 et Q se ferme. La tension de sortie de Q1 décroît donc linéairement, jusqu'à atteindre le seuil V0/3 où la sortie de A2 bascule à 0 et le cycle recommence.
La sortie de A1 va donc osciller entre V0/3 et 2V0/3 (forme d'onde triangulaire) alors que la sortie S de A2 est un signal carré entre 0 et V0.
La durée d'une demi-période est le temps nécessaire pour que la sortie de A1 passe de V0/3 à 2V0/3 (ou inversement).
Le courant de charge ou décharge du condensateur est 
. La tension au bornes de C varie donc avec la pente : 
(on retrouve la constante de temps 2RC). Le temps nécessaire pour varier
de V0/3 est donc :
,
la période de l'oscillation est 
et la fréquence est 
.
C'est une fonction linéaire de vc. Pour R=10 k, C=5 nF on
trouve :
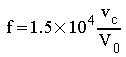
Cet oscillateur peut donc délivrer une fréquence comprise entre 0 et 15 kHz en faisant varier la tension de commande vc.
Dans ce cas, la tension de commande agit sur un composant réactif. Il s'agit du varactor (capacité commandée par une tension)
On utilise la capacité d'une diode polarisée en inverse. Cette capacité dépend de la tension de polarisation.
Des précautions doivent être prises pour insérer ce composant dans le circuit de réaction sélectif.
Exemple : le circuit résonant parallèle de l'oscillateur de Robinson. Il faut isoler le circuit de la tension de polarisation et la tension de commande de l'oscillation. D'où le montage suivant :
Il est possible de modifier la fréquence d'oscillation (et le spectre de cette oscillation) d'un oscillateur sans agir sur ses composants mais en le synchronisant sur un autre oscillateur. Si la synchronisation se produit, sa fréquence et les propriétés de cette fréquence seront imposées par l'oscillateur synchronisant.
Le signal délivré par l'oscillateur synchronisant est appliqué sur une entrée de l'oscillateur à synchroniser.
On peut représenter le montage par le même schéma que celui qui a été utilisé pour étudier l'effet d'une source de bruit. La source de bruit est remplacée par le signal de synchronisation e(t).
La mise en équation reprend les mêmes étapes :
Nous prenons comme état de référence pour l'oscillateur (indice 0) son état lorsque le signal de synchronisation n'existe pas (e(t)=0).
Le point représentatif de cet état est donné par l'intersection
des deux lieux 
et 
:
La pulsation est 
,
l'amplitude 
et le signal de sortie est, dans le domaine temporel :
Le signal de synchronisation est de la forme 
.
Nous nous plaçons dans le domaine temporel et supposons que la pulsation
du
signal de synchronisation est proche de la pulsation de référence
et
que l'amplitude instantanée de 'oscillation est proche de l'amplitude
de référence 
(le signal de synchronisation n'apporte qu'une faible perturbation)
En présence du signal de synchronisation, le signal de sortie voit son
amplitude et sa fréquence légèrement modifiées par
rapport aux valeurs de référence, et on cherche s'il est possible
que cette fréquence soit égale à 
.
,
où
est
le déphasage entre le signal synchronisé et le signal de synchronisation.
Le circuit peut être décrit par l'équation :
soit
:
ou
:
Dans cette dernière relation, nous faisons l'approximation de remplacer A(V) par A(V0) et l'amplitude de s(t) par son expression de référence V0 à droite du signe égal :
Dans le plan de Nyquist, le membre de gauche de cette relation
désigne un vecteur 
qui
a son origine sur la courbe 
pour 
(c'est notre hypothèse) et son extrémité sur la courbe
.
L'état instantané du système est donc décrit
dans le plan de Nyquist par un vecteur issu du point 
et arrivant sur un point de la courbe 
et tel que la relation ci-dessus soit satisfaite. En particulier la longueur
de ce vecteur est imposée : 
La phase du vecteur se déduit du point imposé (sur la courbe B) et de la longueur imposé.
Il n'y aura de solution que si l'origine du vecteur peut être
placée sur la courbe 
: dans l'exemple ci-dessous, il n'y a pas de solution : l'oscillateur ne peut
être synchroniser. Il faudrait diminuer l'écart entre la fréquence
de synchronisation et la fréquence de l'oscillateur livre, ou augmenter
la longueur du vecteur en augmentant l'amplitude du signa de synchronisation.
En assimilant la courbe B à la perpendiculaire à l'axe réel, on peut écrire la condition de synchronisation
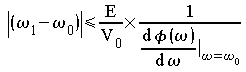
Cette relation donne la condition à satisfaire pour que
la synchronisation puisse avoir lieu, qui fait intervenir la différence
de fréquence et l'amplitude du signal de synchronisation comparée
à l'amplitude de l'oscillateur libre. On constate que la synchronisation
est plus difficile si le circuit sélectif possède un facteur de
qualité élevé (
élevé).
Ce modèle simplifié ne prend pas en compte les effets transitoires. Il permet cependant de prévoir le comportement de l'oscillateur synchronisé : ses écarts (fluctuations) de fréquence contenues dans la plage de synchronisation seront supprimées par la synchronisation si le signal de synchronisation est parfaitement stable. On peut donc s'attendre dans ce cas à un important affinement spectral.
Cette technique est en particulier largement appliquée pour améliorer les propriétés spectrales des lasers de puissance par synchronisation sur un laser de référence.
Contrôle d'un oscillateur par un asservissement de la phase de l'un sur celle de l'autre. La fréquence étant la dérivée de la phase par rapport au temps, une erreur constante d'asservissement n'entraîne pas d'erreur de fréquence.
Pour qu'un tel asservissement puisse être réalisé, il faut :
que l'oscillateur à asservir soit réglable par une tension (VCO),
qu'existe un dispositif qui puisse comparer la phase des deux oscillateurs (comparateur de phase)
Le signal d'erreur est le résultat de la comparaison de la phase de l'oscillateur à asservir et de l'oscillateur. Ce signal est traité par un bloc analogique (filtre) pour obtenir les performances souhaitées et la correction est appliquée sur l'entrée de commande de l'oscillateur à contrôler. La forme la plus simple est donc la suivante :
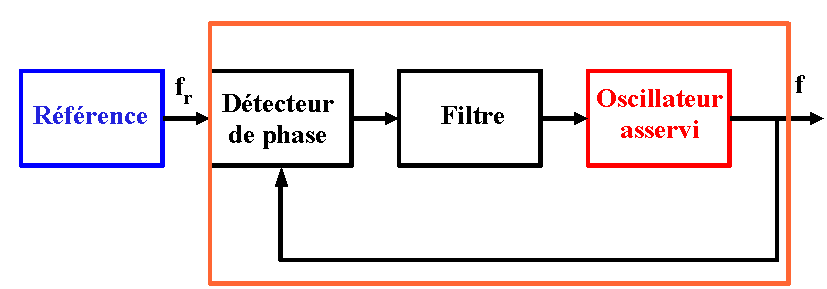
L'entrée du dispositif est la fréquence de référence, la sortie est la fréquence de l'oscillateur asservi. Les grandeurs intermédiaires sont la tension délivrée par le comparateur de phase et la tension délivrée par le filtre.
Des variantes existent qui permettent de mettre en jeu des fréquences (référence et asservie) différentes. Il est ainsi possible d'obtenir une fréquence asservie multiple ou sous multiple de la fréquence de référence, ou une fréquence asservie qui est dans un rapport rationnel avec la fréquence de référence.
Dans l'exemple ci dessus, la fréquence asservie est égale à N fois la fréquence de référence.
Dans l'exemple ci-dessus qui utilise deux diviseurs de fréquence, on peut écrire lorsque l'asservissement est effectif :
, soit
: 
Nous nous limitons au cas le plus simple sans division de fréquence.
Le VCO est modélisé de la façon suivante : la fréquence f du signal qu'il génère est la somme de sa fréquence libre fl (qui peut fluctuer) et de la correction apportée par la tension de contrôle vc :
On suppose le coefficient KVCO (radians par seconde par Volt) indépendant de la fréquence des variations de la tension de commande.
La fréquence du VCO libre est elle-même la somme de sa fréquence nominale F0 et des fluctuations df qui peuvent l'affecter :
Le bloc représentant le VCO peut donc se dessiner ainsi :
Il reçoit deux signaux de fréquences voisines en entrée et délivre une tension en sortie proportionnelle à la différence de phase entre les deux entrées. Kp est le coefficient de proportionnalité (Volts par radian). On le suppose indépendant de la fréquence des variations de la différence de phase.
Sa fonction de transfert est Kf(p).
Elle peut donc être modélisée par le schéma bloc suivant :
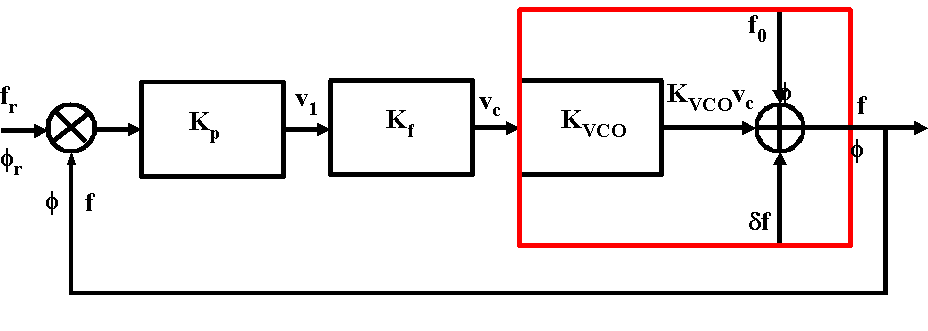
On peut donc écrire les relations suivantes entres les grandeurs intervenant dans le schéma :
Il reste à connecter les fréquences et les phases puisque ces deux grandeurs interviennent dans la description du montage :
La fréquence est la dérivée de la phase : 
.
La relation entre leurs transformées de Laplace est donc :
On peut donc écrire :
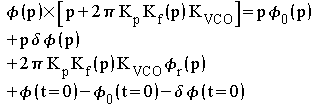
Cette expression fait apparaître les fonctions de transfert qui donnent la dépendance de la phase de l'oscillateur asservi vis à vis des phases des trois entrées et des phases initiales.
Les fonctions de transfert relatives aux fréquences peuvent s'en déduire,
en remarquant que 
(la phase est l'intégrale de la fréquence).
Erreur de phase, pas d'erreur de fréquence
Quelle que soit la fonction de transfert Kf(p) du filtre (non nulle à l'origine), l'effet des phases initiales s'annule aux basses fréquences (p=jw=0) pour l'expression de la fréquence contrôlée terme proportionnel à p). Ce n'est pas le cas de l'expression de la phase asservie : il peut donc exister une différence constante entre la phase asservie et la phase de référence. La fréquence étant la dérivée de la phase, cette erreur de phase n'est pas répercutée sur la fréquence.
. Nous réécrivons donc l'expression ci-dessus relative à la fréquence sans le terme lié aux erreurs de phase :
La fréquence asservie suit la fréquence de référence
Tout au moins si celle-ci ne varie pas vite devant la fréquence de coupure de l'asservissement. Le gain
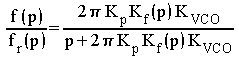tend
en effet vers 1 aux basses fréquences
Les fluctuations de l'oscillateur libre sont atténuées
Le gain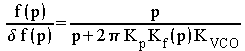 
tend vers 0 aux basses fréquences. Les fréquences élevées
ne sont par contre pas atténuées.
La fréquence nominale ne joue aucun rôle
C'est par convention une fréquence parfaitement constante, qui est donc complètement effacée par l'asservissement (fréquence des fluctuations nulles).
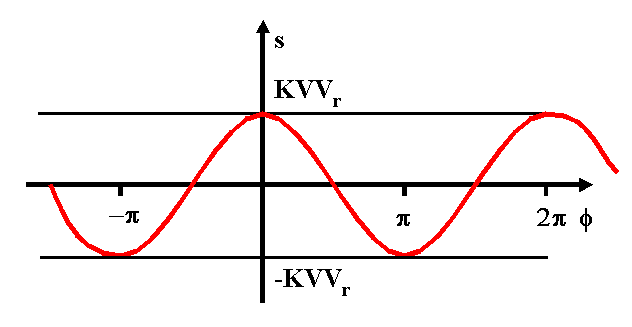
Exemple : comparateur à portes
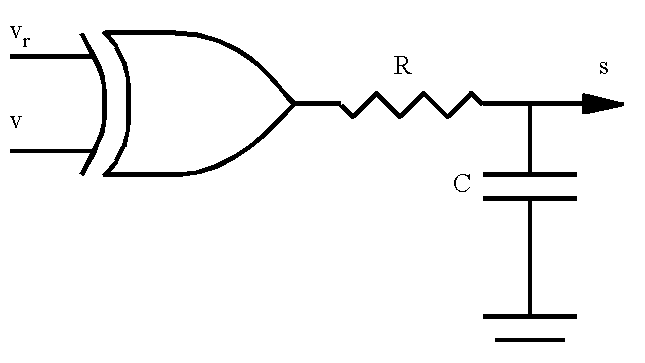
Ce montage simple utilise une porte ou exclusif et délivre une sortie proportionnelle au déphasage f entre v et vr, signaux carrés, pour f compris entre 0 et p.
Soient T la période des signaux, f leur déphasage (déphasage de v par rapport à la référence vr) et v0 la valeur de tension correspondant au niveau logique 1.
Cela signifie que si vr passe
de 0 à 1 à l'instant t0, v passe de 0 à 1 à
l'instant 
.
Pendant une période, l'intervalle de temps où les deux signaux
sont compléments l'un de l'autre est donc :
si 
,
et
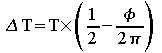si
La valeur moyenne du signal de sortie sur une période , proportionnelle à cette durée, est donc :
La loi de variation de la sortie s en fonction du déphasage est représentée ci-dessous :
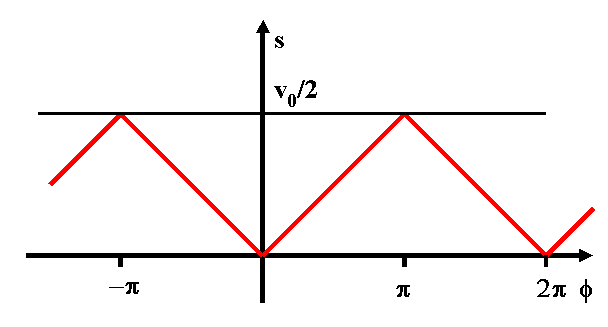
La fonction de transfert de ce bloc n'est donc pas univoque : même valeur de la sortie pour une infinité de valeurs de l'entrée (déphasage). Lorsque l'oscillateur contrôlé est asservi, il faut vérifier que la phase est comprise entre 0 et p. La fonction de transfert est alors connue :
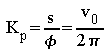
Que se passe-t-il si le déphasage dépasse ces limites (0, p) ?
On réalise alors le produit des deux signaux, qui donne une composante liée à la phase :
Si on construit une troisième tension proportionnelle au produit de ces deux tensions :
Un filtre passe bas permet d'éliminer la composante à la pulsation 2w et de ne conserver que la composante proportionnelle à la phase du signal v par rapport à la référence vr :
Dans ce cas aussi, la fonction de transfert n'est pas univoque et une convention analogue doit être adoptée.
Si les deux fréquences ne sont pas égales, le résultat est un signal à la fréquence différence des deux fréquences (la phase de la sortie varie continûment).
Mélangeur à diode
Si la tension aux bornes d'une diode est vD, son courant iD est de la forme :
avec
l = q/kT=40 à température ambiante
et is de l'ordre de 0.1 mA.
Dans
le montage de la figure ci-dessous, on a 
et donc 
.
On peut écrire 
.
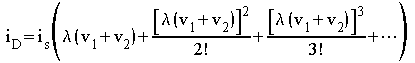Si
on
se limite aux deux premiers termes de ce développement et on a :
Si les deux tensions sont sinusoïdales, le courant dans la diode contient des composantes :
à la fréquence de v1,
à la fréquence de v2
à la fréquence différence des deux fréquences (c'est ce qui nous intéresse ici)
à la fréquence somme des deux fréquences
à la fréquence double de v1
à la fréquence double de v2
à la fréquence nulle
Modulateur en anneau
Le modulateur en anneau (mélangeur équilibré) utilise quatre diodes identiques. Son schéma est représenté ci-dessous.
Le signal e1 est à niveau fort : il dépasse largement le seuil des diodes, toutes identiques. Au contraire, le signal e2 est de faible amplitude, de l'ordre du seuil des diodes.
Au cours des alternances positives, les deux diodes de droite sont passantes et la tension de leur point commun vaut 0 si elles sont identiques. Le point haut du transformateur de droite est donc à 0 et le point bas à -e2.
Au cours des autres alternances, ce sont les diodes de gauche qui conduisent, leur point commun est à 0, et le point bas du transformateur de droite à e2.
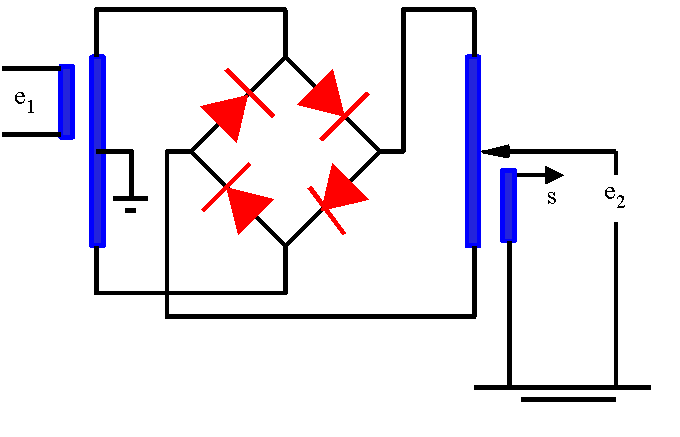
On recueille donc sur le secondaire du transformateur de droite (sortie s) une tension qui reproduit e2, mais avec un changement de signe à la fréquence et à la phase de e1. C'est donc le produit de e2 par un signal carré symétrique entre 1 et -1 dont la fréquence et la phase sont celles de e1(t).
Soit c(t) cette fonction. Elle peut s'écrire sous la forme d'un développement en série de Fourier :
est la pulsation du signal e1.
La pulsation 
du signal e2(t) est
soit voisine de celle du signal e1(t) (cas du détecteur de phase),
soit plus petite que celle du signal e1(t) (cas de la modulation).
Le résultat de ce produit est donc
Cette somme de produits de 2 cosinus se transforme en somme de sommes de 2 cosinus dont les arguments sont la somme et la différence des arguments.
Les composante de plus basse fréquence de ce résultat sont :
Ces deux composantes sont sélectionnées par un filtre passe bas dans le cas de la modulation d'amplitude, seulement celle à la pulsation différence est sélectionnée par un filtre passe bas dans le cas du détecteur de phase.
Si les fréquences sont égales, la composante continue est proportionnelle au cosinus du déphasage.
Le choix du filtre se fait en fonction :
des performances à obtenir
des critères de stabilité à respecter.
Il faut donc étudier la stabilité du montage
Les gains du montage sont donnés par la relation : 
.
Il y a à partir de cette expression deux façons de faire apparaître
un gain en boucle ouverte.
Si nous choisissons de diviser numérateur et dénominateur par
, le
gain en boucle ouverte est :
.
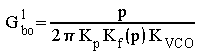Si au contraire on choisit de diviser par p on a :
.
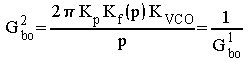Cette expression traduit l'idée physique que l'on se fait de la boucle,
mais la première est tout aussi valable.
On peut envisager quelques cas :
Pas de filtrage
Le filtre est un amplificateur dont la fréquence de coupure est très élevée. Dans ce cas on a
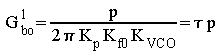ce qui correspond à un filtre passe bas du premier ordre, stable si 
est positif. La seule précaution à prendre est donc relative au
signe de ce produit.
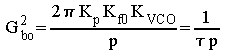
Filtre passe bas du premier ordre
On a 
et 
,
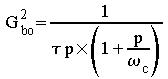
Le diagramme de Bode correspondant à 
est le suivant (en rouge la contribution du filtre passe bas, en bleu celle
du pôle à l'origine (intégrateur parfait) :
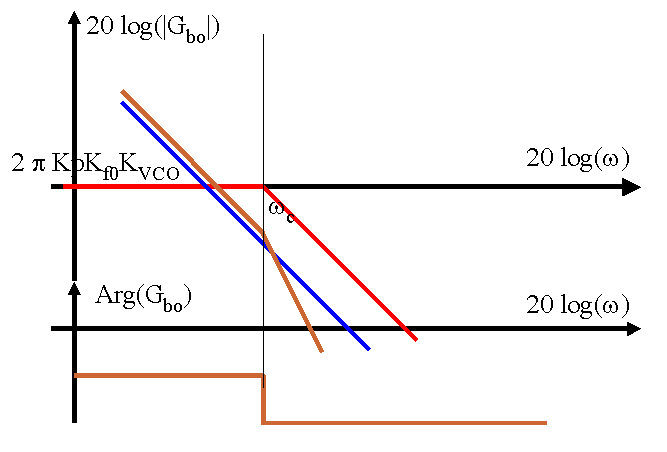
Dans ce cas, la courbe correspondant au demi-cercle de rayon infini est réduite à l'origine. Il y a par contre un pole à l'origine qu'il faut contourner (par un demi-cercle de rayon e par exemple). La partie du lieu de Nyquist qui lui correspond se ferme selon un cercle de rayon 1/e dans le demi-plan de droite. Dans l'exemple, la phase a tourné de moins de 135° lorsque le module atteint la valeur 1. La marge de phase est supérieure à 45°.
Elle est définie par la réponse à la question suivante : L'asservissement étant opérationnel, jusqu'où peut-t-on écarter la fréquence de référence par rapport à la fréquence nominale de l'oscillateur asservi avant que l'asservissement décroche ?
Accordabilité du VCO.
Si la fréquence de référence est est dehors de la plage de fréquences que peut atteindre l'oscillateur à contrôler, l'asservissement ne peut bien sûr pas se maintenir.
Transmittance globale entre le détecteur de phase et le VCO.
Quelle que soit la nature du détecteur de phase, la différence de phase - constante - qu'il donne dans un état donné est compris entre 2 limites (0 et p par exemple pour le détecteur à ou exclusif). À ces valeurs extrêmes correspondent des valeurs extrêmes que peut prendre la fréquence du VCO, la différence entre ces fréquences extrêmes étant le produit des phases extrêmes par la transmittance globale .
L'asservissement décrochera si la fréquence du VCO tente de sortir de ces limites.
Cette plage définit le domaine des fréquences autour de la fréquence de référence à partir desquelles l'asservissement peut s'établir.
Si les fréquences f et fr ne sont pas égales, la sortie du comparateur de phase est un signal périodique, dont la fréquence est la différence des deux fréquences. Ce signal périodique est atténué par le filtre passe-bas, s'il existe, et il est possible qu'il n'atteigne pas la valeur correspondant à la correction de fréquence à appliquer à l'oscillateur.
Pendant une demi-période de ce signal, la tension de commande appliquée sur le VCO rapproche sa fréquence de la fréquence de référence, alors que pendant l'autre demi-période, elle l'éloigne.
Pendant la demi-période où la fréquence de l'oscillateur se rapproche de la fréquence de référence, la fréquence instantanée du signal issu du comparateur de phase diminue, alors qu'elle augmente pendant l'autre demi-période : les deux demi-périodes ne sont donc pas symétriques et l'effet moyen sur une période, compte tenu du filtrage passe bas, est une diminution de la différence des fréquences. La fréquence de l'oscillateur à asservir se rapproche donc de plus en plus de celle de l'oscillateur de référence Il est ainsi possible d'arriver jusqu'à l'égalité des deux fréquences.
Ce mécanisme ne peut se produire que si le signal appliqué sur le VCO est d'amplitude suffisante. La plage de capture peut doncêtre limitée par la bande passante du filtre