Oscillateurs : systèmes non linéaires
Ce chapitre concerne l’étude de systèmes
volontairement instables et dont le comportement est oscillatoire.
Ils constituent les oscillateurs quasi sinusoïdaux qui
fournissent une grandeur électrique dont l’amplitude
oscille périodiquement dans le temps, en l’absence de
toute excitation d’entrée. Le système oscillant
est le plus souvent fortement non linéaire : une méthode
d’étude de systèmes non linéaires est
présentée.
1. Composants non linéaires. Linéarisation.
a. Définitions
Un composant est non linéaire si son équation
fonctionnelle est elle-même non linéaire :
Une résistance, dont l’équation
fonctionnelle
 est linéaire, est un composant linéaire. Si cependant
l’équation fonctionnelle fait intervenir la puissance
troisième du courant :
est linéaire, est un composant linéaire. Si cependant
l’équation fonctionnelle fait intervenir la puissance
troisième du courant :
 ce composant n’est alors pas linéaire (quelle est la
dimension de r ?).
ce composant n’est alors pas linéaire (quelle est la
dimension de r ?).
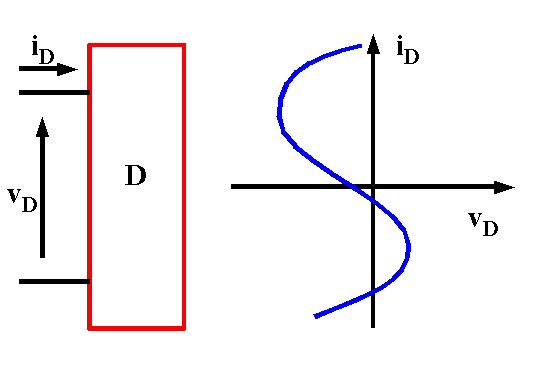
La diode est un composant fortement non linéaire :
son équation fonctionnelle n’est pas représentée
par une droite dans le plan [v,i].
La méthode d’étude que nous adoptons ici est
simple : nous chercherons à linéariser le ou les
composants non linéaires, ce qui est fait habituellement dans
l’approximation des petits signaux.
La résistance ci-dessus est linéarisée et
représentée par le composant linéaire d’équation
 tant que le terme non linéaire
tant que le terme non linéaire
 peut être négligé devant le terme linéaire
peut être négligé devant le terme linéaire
 ,
c’est à dire tant que le courant i (et donc la tension v)
est suffisamment petit :
,
c’est à dire tant que le courant i (et donc la tension v)
est suffisamment petit :
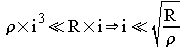
On
retrouve ici l’approximation habituelle des petits signaux.
La
diode peut être représentée lorsqu’elle est
bloquée par une résistance de forte valeur. Lorsqu’elle
est polarisée en direct, elle peut être représentée
par une résistance en série avec une source de tension.
On a donc dans cet exemple aussi linéarisé le
composant, après avoir identifié deux domaines de
fonctionnement différents (diode en inverse, diode en direct).
Une linéarisation différente, donc un schéma
équivalent différent, s’applique dans chacun des
deux domaines.
a. Exemple : résistance négative
C’est un dipôle, caractérisé par une
relation donnant le courant entrant en fonction de la tension à
ses bornes :
indépendante du temps (c'est donc un dipôle
résistif),
dont la courbe représentative présente une
portion de pente est négative. Cette portion est équivalente
à la caractéristique d’une résistance
(éventuellement en série avec une source) mais dont la
valeur est négative.

Dipôle en N
Dipôle en S
La diode tunnel présente une caractéristique de ce
type (en N). On peut également faire la synthèse d’un
tel dipôle, en utilisant par exemple un convertisseur négatif
d’immittance (INIC) et en imposant une non linéarité
:

Un dipôle en S
Lorsque la sortie de l’amplificateur n’atteint pas
les tensions Zener (supposées symétriques +vz
et –vz), le montage se comporte comme un dipôle
dont la caractéristique i(v) est une droite de pente négative
égale à -1/r (résistance négative).
Lorsque l’un ou l’autre des seuils Zener est
atteint, la sortie de l’amplificateur est fixée à
l’une des valeurs +vz eou –vz et le
dipôle est équivalent à la source +vz
ou –vz en série avec la résistance R
(pente 1/R).
La caractéristique globale est en S.

2. Oscillateurs quasi sinusoïdaux : démarrage
L’objectif de ce chapitre est de concevoir et étudier
les propriétés de systèmes réactifs
instables dans lesquels une oscillation quasi sinusoïdale
apparaît spontanément. Son amplitude est croissante
(exponentiellement) tant que le système reste dans le domaine
de l’approximation des petits signaux à l’intérieur
duquel il a été conçu. Lorsque l’amplitude
de l’oscillation devient assez importante pour que des non
linéarité apparaissent, il est possible que l’amplitude
de l’oscillation tende vers une valeur stable. On a alors
fabriqué un oscillateur quasi sinusoïdal.
Nous étudierons ces dispositifs dans les deux cas limites :
-
dans l’approximation des petits signaux, qui est l’approximation
habituelle. Il est alors possible de prévoir leur instabilité
et leur comportement vis à vis d’une impulsion de bruit,
-
dans son régime stabilisé, en supposant qu'il en existe un.
Dans ce régime, l’amplitude de l’oscillation est constante.
Cette étude sera faite en linéarisant le dispositif autour
de son point de fonctionnement dans l’approximation dite du premier
harmonique.
L'étude du démarrage est l’application directe de l’étude
de la stabilité des systèmes du chapitre précédent.
Sur un circuit donné, on va rechercher les conditions qui
le rendent instable : il existe des pôles à
partie réelle positive,
provoquent un comportement oscillatoire (et non pas une
croissance exponentielle monotone vers la tension de saturation) :
il doit donc exister au moins deux pôles complexes
conjugués à partie réelle positive.
Nous envisagerons deux démarche :
le calcul direct des propriétés des pôles,
lorsque c’est possible,
l’étude des propriétés des pôles
par la méthode de Nyquist.
a. Calcul direct des propriétés des pôles d’une fonction
de transfert ou immittance du circuit.
Si on met la fonction de transfert (ou l'immittance) sous la forme
d’une fraction de deux polynômes en p (variable de
Laplace) N(p) et D(p) et si le dénominateur D(p) n’est
pas de degré trop élevé ou possède une
forme que l’on peut traiter analytiquement, il suffit alors
d’étudier les zéros de D(p) puisque ce sont les
pôles de la fonction de transfert. Il faut donc résoudre
l’équation

i. Cas où le degré de D(p) est égal à 2
On a alors à résoudre une équation du
deuxième degré.
Dans ce cas, il y aura deux racines complexes conjuguées à
partie réelle positive si :
le déterminant de l’équation du deuxième
degré est négatif (racines complexes),
la somme des racines, qui vaut deux fois leur partie réelle
est positive.
ii. Cas limite : partie réelle nulle, critère de Barkhausen
Si les pôles sont complexes conjugués mais à
partie réelle nulle (ils sont alors de la forme
 ),
le comportement sera oscillatoire, mais d'amplitude constante
(l’enveloppe de l’oscillation qui apparaît en réponse
à une impulsion de bruit est constante). Cette condition est
obtenue en écrivant l’équation
),
le comportement sera oscillatoire, mais d'amplitude constante
(l’enveloppe de l’oscillation qui apparaît en réponse
à une impulsion de bruit est constante). Cette condition est
obtenue en écrivant l’équation
 ci-dessus et en imposant en plus que les solutions sont de la forme
ci-dessus et en imposant en plus que les solutions sont de la forme
 .
Cette équation s’écrit donc :
.
Cette équation s’écrit donc :

C’est l’expression du critère de Barkhausen.
Cette équation est une équation complexe, qui
recouvre deux équations : il faut annuler la partie
réelle et la partie imaginaire de
 :
:

iii. Exemple : oscillateur de Van der Pol
C’est un dipôle constitué de la mise en
parallèle d’une résistance négative et d’un
circuit résonnant RLC

Oscillateur de Van der Pol
Mise
en équation
Puisqu’on est dans l’approximation linéaire des
petits signaux, le dipôle à résistance négative
est représenté par une résistance de valeur
négative –r et on peut se placer dans le domaine de
Laplace.
Puisque le montage est un dipôle, il est caractérisé
par une immittance. On cherche à établir les conditions
pour lesquelles une tension oscillatoire v prend naissance aux bornes
du circuit, en l’absence de courant extérieur appliqué
i. On calcule donc l’impédance .
Le courant i est la somme des courants passant dans chacun des 4
composants en parallèle :

On a posé G=1/R, g=1/r
et on a donc :

Il faut alors étudier les zéros du dénominateur
de cette impédance, solutions de l’équation du
deuxième degré en p :
 .
.
Critère
de Barkausen
Le critère de Barkhausen s’écrit dans ce cas :
 ,
équation équivalente au système de deux
équations :
,
équation équivalente au système de deux
équations :

qui donnent la pulsation de l’oscillation d’amplitude
constante qui prend naissance en réponse à une
impulsion de bruit et la condition sur g et G pour que l’on soit
dans cette condition limite.
Étude
générale
On aura des pôles complexes conjugués si le
déterminant de cette équation du deuxième degré
en p est négatif :

La partie réelle de ces pôles sera positive ou nulle
si la somme des racines est positive ou nulle :

Ces deux conditions imposent que g soit à l’intérieur
du domaine :

Pour une valeur donnée de g à l’intérieur
de ce domaine, la partie imaginaire des pôles, qui donne la
pseudo pulsation de l’oscillation d’amplitude croissante
qui prend naissance, est donnée par le module du déterminant
divisé par 2 :
 On retrouve bien les résultats donnés à la
limite g=G par le critère de Barkhausen.
On retrouve bien les résultats donnés à la
limite g=G par le critère de Barkhausen.
b. Application de la méthode de Nyquist
Puisqu’on linéarise le système dans la limite
des petits signaux, on est dans les conditions où la méthode
de Nyquist a été établie dans le chapitre
précédent. On peut donc l’appliquer directement
pour étudier l’instabilité du montage. Il est
cependant plus difficile dans le cas général de prévoir
le type d’instabilité (oscillation ou saturation ?).
i. Modification de la présentation du lieu de Nyquist
Habituellement, on représente le lieu du gain en boucle
ouverte Gbo(p) lorsque la variable complexe p parcourt le
contour de Browich (lieu de Nyquist), puis on étudie la
position du point critique de coordonnées -1 et 0 par rapport
à ce lieu.
Il est pratique, pour les applications liées aux
oscillateurs, de mettre le gain en boucle ouverte sous la forme d’un
produit de deux facteurs dont l’un contient la dépendance
en p et l’autre, indépendant de p, dépend en
général du gain du montage :

puis de tracer le lieu de Nyquist de B(p). Il faut alors étudier
ce nouveau lieu, déduit du précédent par une
homothétie, par rapport à un nouveau point critique qui
se déduit du précédent par la même
homothétie : c’est le point critique
 .
Une modification des paramètres de gain du montage se traduit
alors simplement par un déplacement du point critique, sans
qu’il soit nécessaire de retracer le lieu de Nyquist.
.
Une modification des paramètres de gain du montage se traduit
alors simplement par un déplacement du point critique, sans
qu’il soit nécessaire de retracer le lieu de Nyquist.
ii. Nature des pôles à partie réelle positive
On suppose que l’on a pu exploiter pleinement la méthode
de Nyquist, c’est à dire que l’on connaît le
nombre de pôles à partie réelle positive.
Si le nombre de pôles à partie réelle positive
(pprp) est impair, il y a forcément au moins 1 pprp réel.
Cette situation n’est pas favorable au démarrage certain
d’une oscillation.
Si le nombre de pprp est pair, ce sont peut-être tous des
paires de pôles complexes conjugués, mais il est
possible qu’il y ai des paires de pôles réels (de
valeur différente). Dans tous les cas la situation n’est
pas favorable au démarrage d’une oscillation :
plusieurs oscillations peuvent démarrer de façon
concurrente dans le premier cas, le second cas est comparable au cas
impair ci-dessus. Il faut donc se placer (si c’est possible)
dans des conditions qui produisent une seule paire de pprp dont la
position dans le plan complexe détermine les conditions de
démarrage..
Si le nombre de pprp est égal à 2 (cas recommandé
ci-dessus), peut-on savoir s’ils sont complexes conjugués
ou réel ?
Si le lieu de B(p) tourne deux fois autour du point critique
 et que les deux tours se croisent sur l’axe réel, on peut
prévoir qu’en modifiant la valeur de A (supposée
réelle) on fait sortir le point critique des deux tours en
même temps. Les deux pôles ont donc même partie
réelle. Il peut donc s’agir de deux pôles complexes
conjugués ou d’un pôle réel double.
et que les deux tours se croisent sur l’axe réel, on peut
prévoir qu’en modifiant la valeur de A (supposée
réelle) on fait sortir le point critique des deux tours en
même temps. Les deux pôles ont donc même partie
réelle. Il peut donc s’agir de deux pôles complexes
conjugués ou d’un pôle réel double.
iii. Exemple : oscillateur de Robinson
C’est un oscillateur constitué d’une réaction
sélective autour d’un amplificateur de tension.

Oscillateur de Robinson
Le gain en boucle ouverte est facilement calculé en
remarquant que la chaîne d'action (gain k) et la chaîne
de réaction (pont diviseur constitué par R0
et le circuit résonant parallèle) sont facilement
identifiables. Il faut cependant faire attention au signe.
Le gain du pont diviseur est :
 où Z est l’impédance du circuit bouchon et Y son
admittance (gain du pont diviseur). Le gain en boucle ouverte est
donc (attention au signe) :
où Z est l’impédance du circuit bouchon et Y son
admittance (gain du pont diviseur). Le gain en boucle ouverte est
donc (attention au signe) :

On peut alors poser dans les notations précédentes
:A = k et
 .
.
Le calcul de Y(p) donne alors :

Dont le lieu (vérifiez le) est constitué de deux boucles superposées
croisant l’axe horizontal :
en 0 (pour  )
et
)
et
en  (pour
(pour  )
)
Le montage aura donc deux pôles ou aucun pôle à
partie réelle positive selon que le point critique
 est ou non à l’intérieur de cette boucle.
est ou non à l’intérieur de cette boucle.
Il est à l’intérieur (ou à la limite)
pour

![]() est linéaire, est un composant linéaire. Si cependant
l’équation fonctionnelle fait intervenir la puissance
troisième du courant :
est linéaire, est un composant linéaire. Si cependant
l’équation fonctionnelle fait intervenir la puissance
troisième du courant :
![]() ce composant n’est alors pas linéaire (quelle est la
dimension de r ?).
ce composant n’est alors pas linéaire (quelle est la
dimension de r ?).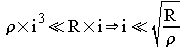








 On retrouve bien les résultats donnés à la
limite g=G par le critère de Barkhausen.
On retrouve bien les résultats donnés à la
limite g=G par le critère de Barkhausen.
 où Z est l’impédance du circuit bouchon et Y son
admittance (gain du pont diviseur). Le gain en boucle ouverte est
donc (attention au signe) :
où Z est l’impédance du circuit bouchon et Y son
admittance (gain du pont diviseur). Le gain en boucle ouverte est
donc (attention au signe) :

 .
.
 (pour
(pour 