Maîtrise et magistère EEA – FIUPSO 2 2002/2003
MODULE EA
TD 8 et TD 9 : Oscillateur à quartz
C'est l'aptitude de l'oscillateur à donner une fréquence proche de sa fréquence nominale. Un oscillateur de fréquence nominale 10 MHz qui délivre une fréquence de 9.5 MHz n'a pas une bonne exactitude. Celui qui donne une fréquence de 9.9995 MHz présente une bonne exactitude.
On caractérise l'exactitude par l'écart relatif entre la grandeur délivrée (ici la fréquence) et sa valeur nominale. On parle alors d'(in)exactitude : le premier des deux exemple présente une inexactitude de 5%, le second une inexactitude de 5 10-5.
C'est l'aptitude de l'oscillateur à reproduire la même fréquence sans ajustement à chaque remise en service. Un oscillateur de bonne reproductibilité, s'il a été correctement calibré, devient un oscillateur de bonne exactitude.
Caractérise la façon dont la fréquence délivrée varie dans le temps ou en fonction de paramètres de l'environnement tel que la température.. Diverses grandeurs permettent de quantifier la stabilité, elles s'expriment en valeur relative. Une (in)stabilité de 2 10-3 indique que la fréquence fluctue dans le temps en s'écartant de moins de 10-3 de sa valeur moyenne.
On dispose d'une bande B de 1 MHz autour d'une porteuse à 10 MHz pour transmettre un certain nombre d'informations. Chacune de ces informations (un canal) occupe un spectre de ± 10 kHz autour d'une sous porteuse. Les sous porteuses sont réparties régulièrement sur la bande B, la fréquence de chacune d'entre elles est proche de 10 MHz .
Chacune des sous porteuses possède une inexactitude E et une instabilité S :
E est l'écart relatif maximal entre la fréquence réelle et la fréquence nominale de l'oscillateur délivrant la porteuse,
S est l'amplitude maximale des fluctuations de fréquence au cours du temps.
Pour assurer l'intégrité des informations, il est bien sûr nécessaire que les spectres ne se recouvrent à aucun moment
Combien de canaux peut-on faire transiter dans la bande B dans les deux cas suivants :
E=S=0,1%
E=S=10-6
Quelle conclusion en tirer ?
Le quartz est un matériau piézo-électrique : soumis à une contrainte, une tension apparaît sur ses faces, soumis à un champ électrique, il subit une déformation.
Un résonateur à quartz est constitué d'une plaquette de quartz taillée convenablement et placée entre deux électrodes. La plaquette de quartz est un système vibrant mécanique qui se trouve relié, grâce à l'effet piézo-électrique au monde de l'électricité : le composant placé entre les deux électrodes est un système résonant électrique, qui présente des propriétés remarquables
Il est rappelé sur la figure suivante :
Il est constitué d'un circuit résonnant série, qui traduit la résonance mécanique de la plaquette de quartz, en parallèle avec un condensateur qui représente la capacité entre les deux électrodes.
Ce circuit résonnant série présente des propriétés remarquables :
Son facteur de qualité Q est élevé
Son condensateur C est de très faible valeur, qui serait irréalisable par un condensateur réel
Son inductance L est de forte valeur, qui serait irréalisable dans le même volume et avec une si petite résistance par un bobinage réel
Voici des ordres de grandeur pour un composant de grande diffusion :
Nous prendrons pour nos applications numériques : r = 50 W, C = 5 fF, C0 = 2 pF (fF : femto Farad = 10-15 Farad) et une fréquence fs de résonance du circuit série de 10 MHz.
Calculer avec ces ordres de grandeur :
La valeur de l'inductance L
Le coefficient de qualité Q
Le rapport a = C/C0 qui joue un rôle important dans la description du circuit équivalent.
Calculer cette impédance dans l'espace des pulsations w.
Monter que cette impédance met en évidence deux pulsations caractéristique du composant :
La pulsation ws de résonance série du circuit série
Une pulsation wp séparée de ws par la quantité C/2C0=a/2 en valeur relative et qui correspond à une résonance parallèle.
On se place successivement au voisinage de chacune des deux pulsations caractéristiques ci-dessus. Les ordres de grandeur permettent un certain nombre de simplifications :
La séparation entre les deux pulsations
caractéristiques est faible en valeur relative :
On étudie le comportement de l'impédance
(ou de l'admittance) au voisinage de chacune de ces deux pulsations
en respectant les conditions :
pour l'étude autour de ws
et
pour l'étude autour de wp.
Monter que dans ces conditions, l'impédance du résonateur à quartz peut se mettre sous la forme :
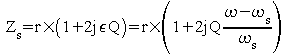
En déduire la pente
des variations de la phase de cette impédance au voisinage de
la résonance série.
Quelle est la valeur numérique de la résistance équivalente au quartz à la résonance série ?
Monter que dans les conditions ci-dessus, l'impédance du résonateur à quartz peut se mettre sous la forme :
En déduire la pente
des variations de la phase de cette impédance au voisinage de
la résonance parallèle.
Quelle est la valeur numérique de la résistance équivalente au quartz à la résonance parallèle ?
Le calcul numérique de l'impédance du circuit équivalent du résonateur avec les valeurs numériques ci dessus donne les résultats suivants :
Ci dessous une portion de la courbe dilatée au voisinage de la résonance série :
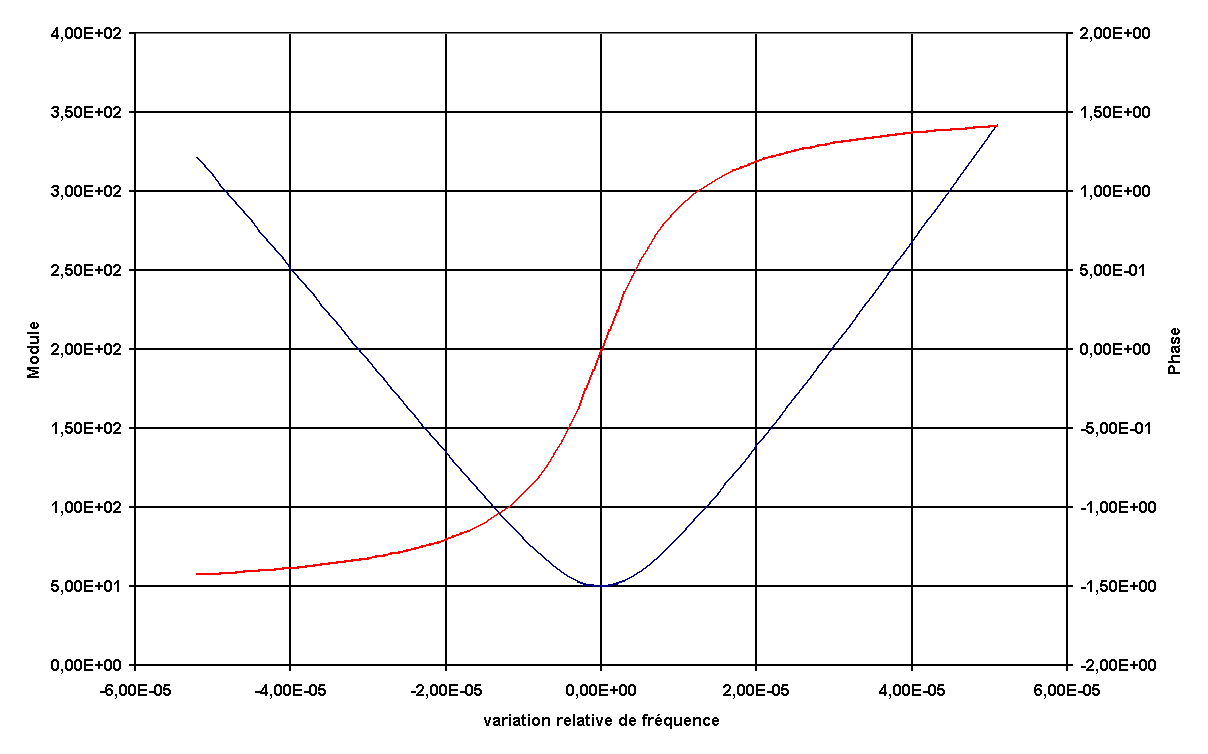Comparez
avec les résultats de vos calculs.
Le résonateur à quartz est inséré dans la chaîne de réaction de telle sorte que le gain en boucle ouverte entoure le point critique et traverse l'axe réel au voisinage d'une des deux fréquences caractéristiques du résonateur.
Analysez le schéma de la figure ci-dessus en faisant la remarque que le gain de boucle sera maximal en module au voisinage de la résonance série du résonateur. On le représentera donc par Zs.
G est une source de courant parfaite commandée
par la tension d'entrée ve :
.
Calculez le gain en boucle ouverte du montage en fonction de ZQ, Z1 et Z2.
Explicitez ce gain en boucle ouverte lorsque Z1 est un condensateur C1 et Z2 un condensateur C2 et lorsque l'on est au voisinage de la résonance série (utiliser la forme Zs trouvée ci-dessus).
La phase du gain en boucle ouverte peut-elle prendre la valeur p (correspondant au critère de Barkhausen) au voisinage de la résonance série ?
Quel doit être le signe de la transconductance g.
Quelle est la valeur de la fréquence qui réalise cette condition ?
Quelle est alors la valeur limite de la transconductance g de la source commandée.
Comment régler la fréquence de l'oscillation ?
Quelle est la sensibilité de la fréquence de l'oscillateur aux valeurs des condensateurs ?
Quelle est la pente
au voisinage de la fréquence d'oscillation ?
Que se passe-t-il si C1 subit une variation de 10% ?
Les caractéristiques du résonateur qui nous a servi d'exemple sont les suivantes :
Imprécision sur la fréquence : ± 50 10-6
Sensibilité à la température : ± 0.4 10-6 /°
Dérive de fréquence sur la première année (vieillissement) : ± 3 10-6
Quelles sont les propriétés de vieillissement et de stabilité thermique de ces oscillateurs ?
Comment ramener la fréquence de l'oscillateur à sa valeur nominale (à 10-6 près) s'il s'en écarte de 50 10-6 ?
Le montage de la figure suivante est celui d'un oscillateur de Pierce en émetteur commun.
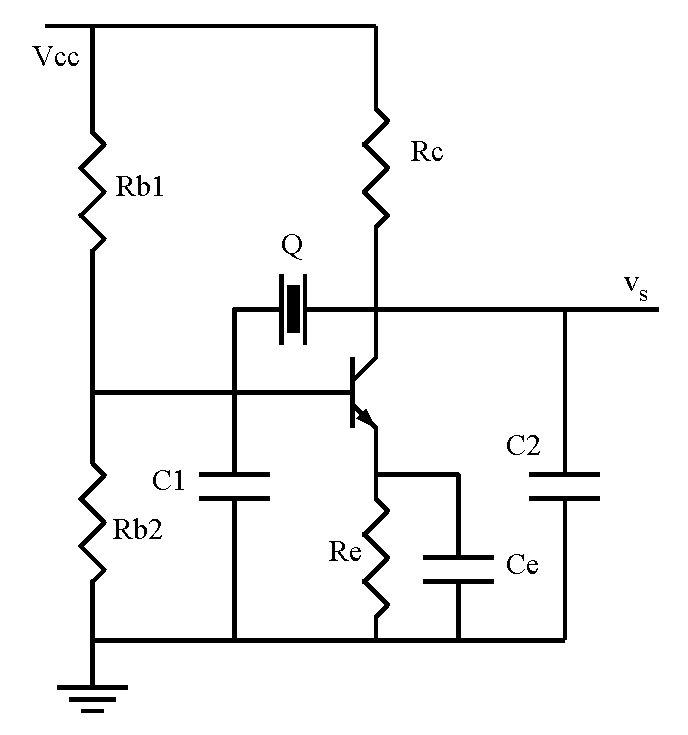
Rb1, Rb2, Rc et Re assurent la polarisation correcte du transistor bipolaire.
Le résonateur, C1 (en parallèle avec Rb1 et Rb2) et C2 (en parallèle avec Rc constituent la chaîne de rétroaction. Les valeurs de C1 et C2 tiennent compte des capacités parasites du transistor.
Le condensateur Ce connecte l'émetteur à la masse pour la fréquence de travail (10 MHz).
On suppose que la tension continue d'alimentation est de 15 V, que la tension continue entre émetteur et collecteur est de 5 V, ainsi que la tension aux bornes de Rc. Le courant collecteur est de 0.5 mA.
En déduire les valeurs à choisir pour Rc, Re et Ce.
Choisir les valeurs de Rb1 et Rb2, de l'ordre de quelques kW chacune.
On adoptera le schéma équivalent petits signaux le plus simple pour le transistor : une source de courant commandée par la tension base-émetteur, une résistance d'entrée grande devant les résistance choisies pour le pont de polarisation de la base. Le schéma équivalent petits signaux du montage est donc le suivant :
Calculer le gain en boucle ouverte en fonction de l'impédance ZQ du résonateur, de l'impédance Z1 constituée par C1 en parallèle avec les résistances du pont de polarisation de la base, de l'impédance Z2 constituée de C2 en parallèle avec la résistance Rc et de la transconductance g.
Si une oscillation se produit, de quelle résonance du résonateur sera-telle proche ?
En utilisant l'expression de l'impédance du résonateur proche de la résonance choisie, appliquer le critère de Barkhausen pour déterminer la fréquence de l'oscillation.
Quelle est la valeur limite de g qui assure l'oscillation ?