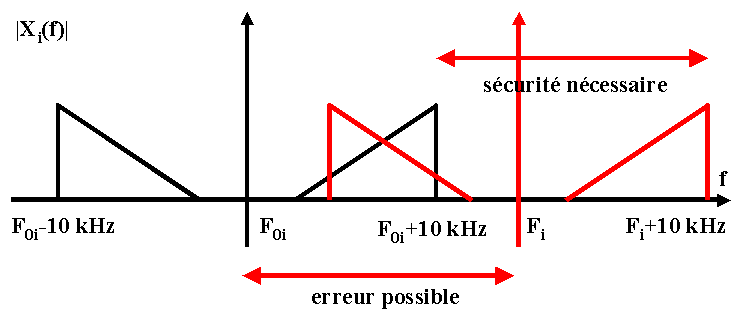
Le spectre de l'information numéro i est centré sur la fréquence nominale F0i et occupe une bande de ± 10 kHz autour de F0i.La fréquence réelle Fi de la sous-porteuse diffère de la fréquence nominale du fait
de l'inexactitude E de l'oscillateur qui la génère. L'écart peut être dans le pire des cas ± F01E
de l'instabilité S de l'oscillateur qui la génère. Les fluctuations de fréquences peuvent écarter la fréquence réelle de la quantité supplémentaire F01S
Dans le pire des cas, la fréquence réelle de chaque sous porteuse peut donc s'écarter de sa valeur nominale de
Chacun des spectres doit donc être séparé
des voisins par un intervalle de sécurité de
.
L'encombrement de chaque voie est donc la somme de l'encombrement
nominal (20 kHz dans l'exemple) et de
On a alors
et chaque voie occupe 60 kHz. On ne peut donc placer que 16 voies
dans la bande de 1 MHz
On a alors
et chaque voie occupe 20.04 kHz. On peut alors placer 49 voies dans
la bande de 1 MHz
La valeur de l'inductance L
Le coefficient de qualité Q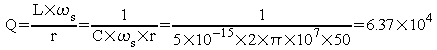
Le rapport a =
C/C0 qui joue un rôle important dans la description
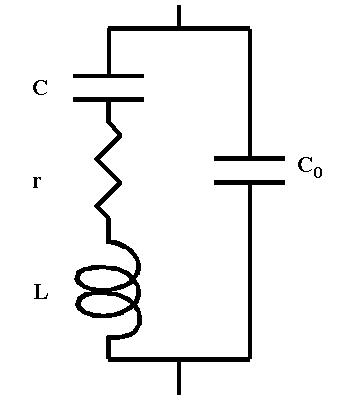
du circuit équivalent.
Un circuit résonant série shunté par la capacité inter électrodes C0.
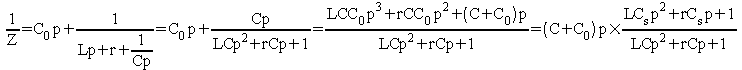
Dans cette expression, Cs est la capacité qui résulte de la mise en série de C et C0 :
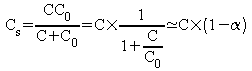
Compte tenu des ordres de grandeur, le condensateur résultant de la mise en série des deux condensateurs (CC0/C+C0) est très peu différent du condensateur C.
On a alors :
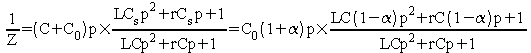
La pulsation ws
de résonance série du circuit série annule la
partie réelle du dénominateur :
La pulsation wp
annule la partie réelle du numérateur : 
On a donc
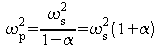et
On est au voisinage de ws. On pose donc
avec
et on peut écrire
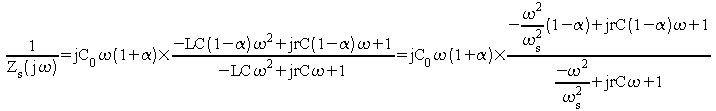
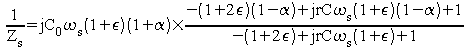
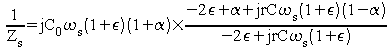
On a
On peut donc écrire avec une très bonne approximation :
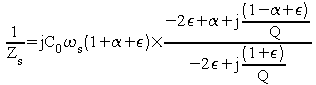
et en négligeant les termes petits devant 1 dans les parties imaginaires de la fraction ainsi que le terme indépendants de la fréquence et petit devant 1dans le premier facteur :
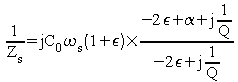
Si on ne s'approche pas de la résonance
parallèle on a de plus :
et
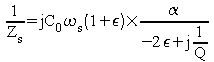ce qui peut s'écrire :
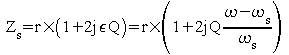
Il est alors facile de répondre aux questions posées :
La phase de cette impédance est donnée par :
et au voisinage de la résonance on peut écrire :
et la pente de ses variations en fonction de la pulsation est :
.
Elle est proportionnelle au facteur de qualité Q.
Le module est minimal pour
et vaut r, comme on pouvait s'y attendre pour une résonance
série (quelle est l'influence de la capacité C0
?)
Le calcul fait appel aux mêmes approximations.
On est au voisinage de wp. On pose donc
Cette fois ci,
est l'écart relatif de fréquence par rapport à
la résonance parallèle.
La pulsation de résonance est définie
par :
et on peut écrire
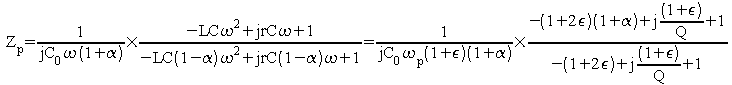
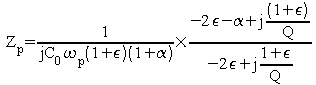
En faisant des simplifications comme ci dessus :
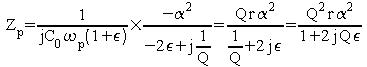
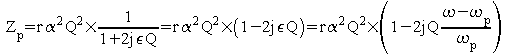
La phase est donnée par la même expression (au signe près) que pour la résonance série.
La résistance équivalente au quartz à la résonance parallèle est :
Les valeurs de résistance aux résonances coïncident très bien. On peu de plus tracer les courbes correspondant aux expressions trouvée pour comparer aux résultats du calcul numérique.
On a les deux équations représentant la boucle :
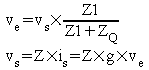
où Z est l'impédance offerte à vs par Z2, Q et Z1 :
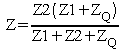
et où la charge est supposée ne pas perturber le fonctionnement du dispositif.
Le gain en boucle ouverte est donc :
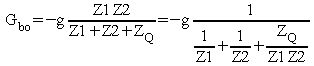
Si
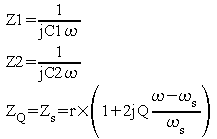
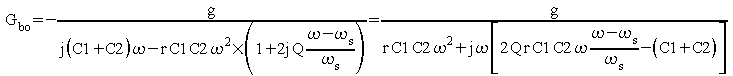
soit, en posant
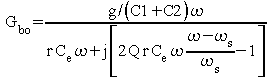
La partie imaginaire du gain en boucle ouverte s'annule pour
,
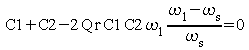soit pour :
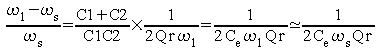
ou bien , en faisant apparaître le rapport entre la capacité C et Ce :
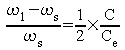
En prenant C1=C2=20 pF comme ordre de grandeur on obtient :
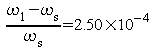
Le gain en boucle ouverte est donc réel pour une fréquence supérieure à la résonance série et très proche de cette résonance. Il vaut alors :
La valeur limite gl de g qui satisfait le critère de Barkhausen est donc :
La phase est donnée, au voisinage de la fréquence d'oscillation, par :
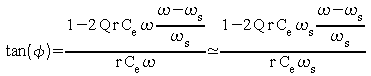
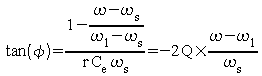et on a comme pour le quartz seul :
Que se passe-t-il si C1 et C2 subissent la même variation variation de 10% ?
Dans ce cas, Ce subit la même variation de 10% et l'écart relatif de la fréquence d'oscillation par rapport à la fréquence de résonance subit également une variation de 10% environ. La variation relative de fréquence de l'oscillation est donc égale à 10% de 2.5 10-4, soit 2.5 10-5
Quelles sont les propriétés de vieillissement et de stabilité thermique de ces oscillateurs ?
Pratiquement celles du résonateur (cf petit calcul ci-dessus)
Ramener la fréquence de l'oscillateur à sa valeur nominale (à 10-6 près) s'il s'en écarte de 50 10-6 ?
Une méthode habituelle : placer un condensateur en série avec le résonateur : 20 pF déplacent la résonance série de 114 10-6
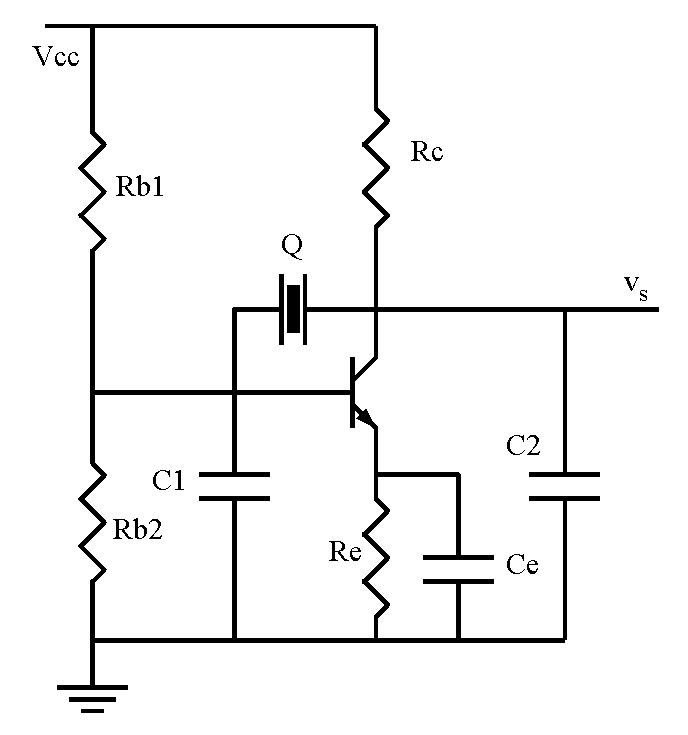
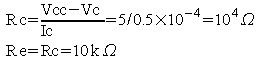
On peut prendre Ce = 100 pF
Choisir les valeurs de Rb1 et Rb2, de l'ordre de quelques kW chacune.
où Rb'2 est la mise en parallèle de Rb2 et Rp
On peut prendre Rb'2=4 kW, Rb1=6.7 kW, Rb2=20 kW. La mise en parallèle de ces 3 résistances donne 2.23 kW
On a les deux équations représentant la boucle :
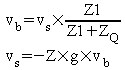
où Z est l'impédance offerte à vs par Z2, Q et Z1 :
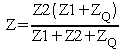
Le gain en boucle ouverte est donc :
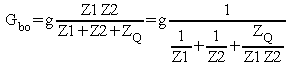
Comme pour l'exemple simple précédent, on suppose que l'oscillation sera proche de la résonance série, ce qui permet de représenter l'impédance du résonateur par l'expression correspondante :
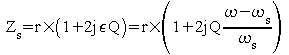
On a de plus :
On a donc :
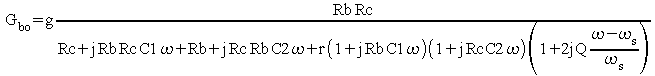
On peut comme précédemment remplacer w par ws partout ou sa différence avec ws n'apparaît pas :
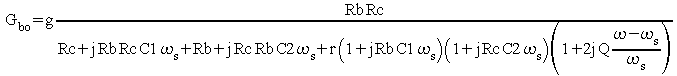
Le gain en boucle ouvert est réel pour :
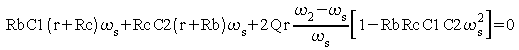
soit :
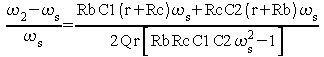
Avec les valeurs numériques suivantes :
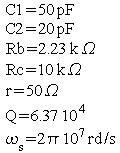
on trouve
,
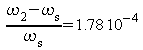valeur proche de la précédente.
Le gain en boucle ouverte vaut alors :
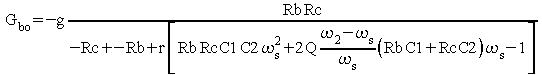
La valeur limite de g es t donc :
